二叉搜索树

前言

二叉搜索树「中序遍历」得到的值构成的序列一定是升序的

验证二叉搜索树

题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。节点的右子树只包含大于当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3] 输出：true 示例 2：

输入：root = [5,1,4,null,null,3,6] 输出：false 解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 10^4] 内 -2^31 <= Node.val <= 2^31 - 1

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/validate-binary-search-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

暴力递归

如果不利用BST的性质的话，根据BST的定义可以有：

当前节点的值要比其左子树节点所有的值都要大，即大于左子树中最大的值

当前节点的值要比其右子树节点所有的值都要小，即小于右子树中最小的值

左右子树也要是BST

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<TreeNode*,int> maxValue,minValue;
    int getMaxvalue(TreeNode* root){
        if(maxValue.count(root)) return maxValue[root];
        if(!root->left && !root->right) {
            maxValue.emplace(root,root->val);
            return root->val;
        }
        int res=root->val;
        if(root->left) res = max(res,getMaxvalue(root->left));
        if(root->right) res = max(res,getMaxvalue(root->right));
        maxValue.emplace(root,res);
        return res;
    }
    int getMinvalue(TreeNode* root){
        if(minValue.count(root)) return minValue[root];
        if(!root->left && !root->right) {
            minValue.emplace(root,root->val);
            return root->val;
        }
        int res=root->val;
        if(root->left) res = min(res,getMinvalue(root->left));
        if(root->right) res = min(res,getMinvalue(root->right));
        minValue.emplace(root,root->val);
        return res;
    }
    bool isValidBST(TreeNode* root) {
        if(!root) return true;
        bool res = true;
        
        if(root->left) res = res && root->val>getMaxvalue(root->left) &&isValidBST(root->left);

        if(root->right) res = res && root->val<getMinvalue(root->right) && isValidBST(root->right);

        return res;
    }
};

更聪明的递归

设计递归函数helper(root,lower,upper)表示根节点为root的子树中，所有的节点值的范围是否在(lower, upper)范围内

根据二叉搜索树的性质，在递归调用左子树时，上界需改为root->val；在递归调用右子树时，下界需改为root->val。

注意最开始时的初始化

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
public:
    bool helper(TreeNode* root, long long lower, long long upper) {
        if (root == nullptr) {
            return true;
        }
        if (root -> val <= lower || root -> val >= upper) {
            return false;
        }
        return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
    }
    bool isValidBST(TreeNode* root) {
        return helper(root, LONG_MIN, LONG_MAX);
    }
};

中序遍历

知道二叉搜索树「中序遍历」得到的值构成的序列一定是升序的，这启示我们在中序遍历的时候实时检查当前节点的值是否大于前一个中序遍历到的节点的值即可。

迭代

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> stk;
        long long pre = (long long)INT_MIN-1;
        TreeNode* cur = root;
       
        while(stk.size()||cur!=nullptr){
            while(cur!=nullptr){
                stk.push(cur);
                cur = cur->left;
            }
            cur = stk.top();
            stk.pop();
           
            if(cur->val <= pre) return false;
            else pre = cur->val;

            cur = cur->right;
        }
        
        return true;
    }
};

递归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    long long pre = (long long)INT_MIN-1;
    bool isValidBST(TreeNode* root) {
        if(!root) return true;
        
        if(!isValidBST(root->left)) return false;
        if(root->val <= pre) return false;
        else pre = root->val;

        return isValidBST(root->right);
    }
};

二叉树的最近公共祖先

题目

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出：3 解释：节点 5 和节点 1 的最近公共祖先是节点 3 。示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出：5 解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。示例 3：

输入：root = [1,2], p = 1, q = 2 输出：1

提示：

树中节点数目在范围 [2, 10^5] 内。 -10^9 <= Node.val <= 10^9 所有 Node.val 互不相同。 p != q p 和 q 均存在于给定的二叉树中。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

递归

如果root是p,q的最近公共祖先，则有以下几种情况：

1）p和q在root的子树中，且分列root的异侧（分别在左、右子树中）

2）p=root，且q在root的左或右子树中

3）q=root，且p在root的左或右子树中

明白lowestCommonAncestor(root,p,q)的作用：返回以root为根的子树中，节点p和q的最近公共祖先。

相信它能完成，那么

考虑边界，当root为空时，返回nullptr；当p或q就为root时，返回root。

考虑下一层，L=左子树中节点p和q的最近公共祖先，R=右子树中节点p和q的最近公共祖先。如果!L即左子树中没找到p和q的最近公共祖先，那就返回在右子树中找到的结果，如果!R即在右子树中没找到p和q的最近公共祖先，那就返回在左子树中找到的结果，如果!L && !R即左右子树中都没找到，说明没有（题目给定p和q均在给定的二叉树中），如果L && R即左右子树中都找到了，说明p、q在root的异侧，返回root。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==NULL || p==root || q==root) return root;
        TreeNode* L = lowestCommonAncestor(root->left,p,q);
        TreeNode* R = lowestCommonAncestor(root->right,p,q);
        if(!L) return R;
        else if(!R) return L;
        else return root;
    }
};

存储父节点

用哈希表存储所有节点的父节点，利用父节点的节点信息从p节点不断往上跳，并记录，再从q节点不断往上跳，如果碰到了已经访问过的节点，则该节点就是最近公共祖先。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    unordered_map<int, TreeNode*> fa;
    unordered_map<int, bool> vis;
    void dfs(TreeNode* root){
        if (root->left != nullptr) {
            fa[root->left->val] = root;
            dfs(root->left);
        }
        if (root->right != nullptr) {
            fa[root->right->val] = root;
            dfs(root->right);
        }
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        fa[root->val] = nullptr;
        dfs(root);
        while (p != nullptr) {
            vis[p->val] = true;
            p = fa[p->val];
        }
        while (q != nullptr) {
            if (vis[q->val]) return q;
            q = fa[q->val];
        }
        return nullptr;
    }
};

二叉搜索树的最近公共祖先

题目

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉搜索树中。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

递归

这题完全可以复制上一题的代码。

如果利用二叉搜索树的性质的话：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==NULL || p==root || q==root) return root;
        if(p->val < root->val && q->val < root->val) return lowestCommonAncestor(root->left,p,q);
        else if(p->val > root->val && q->val > root->val) return lowestCommonAncestor(root->right,p,q);
        else return root;
    }
};

迭代

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        TreeNode* ancestor = root;
        while (true) {
            if (p->val < ancestor->val && q->val < ancestor->val) {
                ancestor = ancestor->left;
            }
            else if (p->val > ancestor->val && q->val > ancestor->val) {
                ancestor = ancestor->right;
            }
            else {
                break;
            }
        }
        return ancestor;
    }
};

二叉搜索树的插入操作

题目

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回任意有效的结果。

示例 1：

输入：root = [4,2,7,1,3], val = 5 输出：[4,2,7,1,3,5] 解释：另一个满足题目要求可以通过的树是：

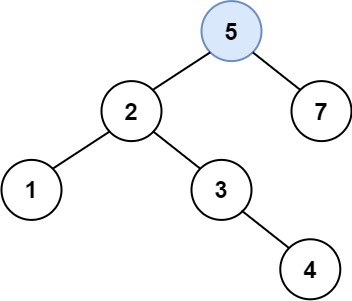
示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25 输出：[40,20,60,10,30,50,70,null,null,25] 示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 输出：[4,2,7,1,3,5]

提示：

树中的节点数将在 [0, 10^4]的范围内。 -10^8 <= Node.val <= 10^8 所有值 Node.val 是独一无二的。 -10^8 <= val <= 10^8 保证 val 在原始BST中不存在。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/insert-into-a-binary-search-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

递归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root==nullptr) root = new TreeNode(val);
        if(val < root->val) root->left = insertIntoBST(root->left,val);
        else if(val > root->val) root->right = insertIntoBST(root->right,val);
        return root;
    }
};

迭代

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root==nullptr) return new TreeNode(val);

        TreeNode* res = root;

        while(root){
            if(val > root->val){
                if(root->right) root = root->right;
                else {
                    root->right = new TreeNode(val);
                    break;
                }
            }else if(val < root->val){
                if(root->left) root = root->left;
                else{
                    root->left = new TreeNode(val);
                    break;
                }
            }
        }

        return res;
    }
};

删除二叉搜索树中的节点

题目

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；如果找到了，删除它。

示例 1:

输入：root = [5,3,6,2,4,null,7], key = 3 输出：[5,4,6,2,null,null,7] 解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。另一个正确答案是 [5,2,6,null,4,null,7]。

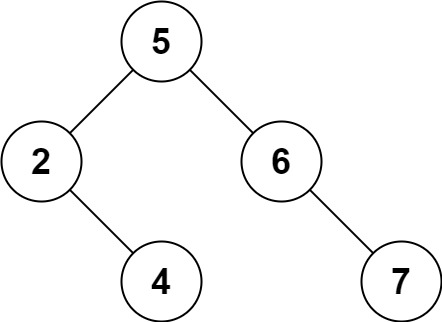
示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0 输出: [5,3,6,2,4,null,7] 解释: 二叉树不包含值为 0 的节点示例 3:

输入: root = [], key = 0 输出: []

提示:

节点数的范围 [0, 10^4]. -10^5 <= Node.val <= 10^5 节点值唯一 root 是合法的二叉搜索树 -10^5 <= key <= 10^5

进阶：要求算法时间复杂度为 O(h)，h 为树的高度。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/delete-node-in-a-bst 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

递归1.0

有以下五种情况：

第一种情况：没找到删除的节点，遍历到空节点直接返回了
找到删除的节点
- 第二种情况：左右孩子都为空（叶子节点），直接删除节点，返回NULL为根节点
- 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
- 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
- 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(!root) return nullptr;
        if(root->val == key){
            if(root->left==nullptr && root->right==nullptr){
                return nullptr;
            }else if(root->left==nullptr && root->right!=nullptr){
                return root->right;
            }else if(root->right==nullptr && root->left!=nullptr){
                return root->left;
            }else{
                TreeNode* cur = root->right;
                while(cur->left) cur = cur->left;
                cur->left = root->left;
                return root->right;
            }
        }
        
        else if(key > root->val) root->right = deleteNode(root->right, key);
        else if(key < root->val) root->left = deleteNode(root->left, key);

        return root;
    }
};

这种方法虽然能过，但是树的高度一直在增加

递归2.0

官方题解，通过替换删除节点和前驱节点或后继节点的值，然后一直递归删除来达到目的

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
  /*
  One step right and then always left
  */
  public int successor(TreeNode root) {
    root = root.right;
    while (root.left != null) root = root.left;
    return root.val;
  }

  /*
  One step left and then always right
  */
  public int predecessor(TreeNode root) {
    root = root.left;
    while (root.right != null) root = root.right;
    return root.val;
  }

  public TreeNode deleteNode(TreeNode root, int key) {
    if (root == null) return null;

    // delete from the right subtree
    if (key > root.val) root.right = deleteNode(root.right, key);
    // delete from the left subtree
    else if (key < root.val) root.left = deleteNode(root.left, key);
    // delete the current node
    else {
      // the node is a leaf
      if (root.left == null && root.right == null) root = null;
      // the node is not a leaf and has a right child
      else if (root.right != null) {
        root.val = successor(root);
        root.right = deleteNode(root.right, root.val);
      }
      // the node is not a leaf, has no right child, and has a left child    
      else {
        root.val = predecessor(root);
        root.left = deleteNode(root.left, root.val);
      }
    }
    return root;
  }
}

删除节点再创建

这种解法也行

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
TreeNode *creat(vector<TreeNode*> &mid,int l,int r)
{
    if(l>r) return nullptr;
    int m=l+((r-l)>>1);
    TreeNode *root=mid[m];
    root->left=creat(mid,l,m-1);
    root->right=creat(mid,m+1,r);
    return root;
}
    TreeNode* deleteNode(TreeNode* root, int key) {
        vector<TreeNode*> mid;
        stack<TreeNode*> s;
        while(!s.empty()||root)
        {
            while(root)
            {
                s.push(root);
                root=root->left;
            }
            root=s.top();
            s.pop();
            if(root->val!=key)
            {
                mid.push_back(root);
            }
            root=root->right;
        }
        root=creat(mid,0,mid.size()-1);
        return root;

    }
};

普通二叉树的删除

和递归2.0中思路类似，找到删除节点后，如果没右子节点了，返回左子节点即可。如果有右子节点，则和右子树最左节点交换值，再递归删除。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return root;
        if (root->val == key) {
            if (root->right == nullptr) { // 这里第二次操作目标值：最终删除的作用
                return root->left;
            }
            TreeNode *cur = root->right;
            while (cur->left) {
                cur = cur->left;
            }
            swap(root->val, cur->val); // 这里第一次操作目标值：交换目标值其右子树最左面节点。
        }
        root->left = deleteNode(root->left, key);
        root->right = deleteNode(root->right, key);
        return root;
    }
};

修剪二叉搜索树

题目

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在唯一的答案。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

输入：root = [1,0,2], low = 1, high = 2 输出：[1,null,2] 示例 2：

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3 输出：[3,2,null,1]

提示：

树中节点数在范围 [1, 10^4] 内 0 <= Node.val <= 10^4 树中每个节点的值都是唯一的题目数据保证输入是一棵有效的二叉搜索树 0 <= low <= high <= 10^4

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/trim-a-binary-search-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

递归

利用好二叉搜索树的性质，明白递归函数的作用

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root == nullptr) return root;

        if(root->val >= low && root->val <= high){
            root -> left = trimBST(root->left, low, high);
            root -> right = trimBST(root->right, low, high);

        }
        else if(root->val < low )
            return trimBST(root->right,low,high);
        else if(root->val > high)
            return trimBST(root->left,low,high);

        return root;
        
    }
};

迭代

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int L, int R) {
        if (!root) return nullptr;

        // 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭
        while (root != nullptr && (root->val < L || root->val > R)) {
            if (root->val < L) root = root->right; // 小于L往右走
            else root = root->left; // 大于R往左走
        }
        TreeNode *cur = root;
        // 此时root已经在[L, R] 范围内，处理左孩子元素小于L的情况
        while (cur != nullptr) {
            while (cur->left && cur->left->val < L) {
                cur->left = cur->left->right;
            }
            cur = cur->left;
        }
        cur = root;

        // 此时root已经在[L, R] 范围内，处理右孩子大于R的情况
        while (cur != nullptr) {
            while (cur->right && cur->right->val > R) {
                cur->right = cur->right->left;
            }
            cur = cur->right;
        }
        return root;
    }
};

将有序数组转换为二叉搜索树

题目

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵高度平衡二叉搜索树。

高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

输入：nums = [-10,-3,0,5,9] 输出：[0,-3,9,-10,null,5] 解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

输入：nums = [1,3] 输出：[3,1] 解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

1 <= nums.length <= 10^4 -10^4 <= nums[i] <= 10^4 nums 按严格递增顺序排列

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

递归

想象一下线段树

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* build(vector<int>& nums,int l, int r){
        if(l>r) return nullptr;
        int mid = (l+r)/2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = build(nums,l,mid-1);
        root->right = build(nums,mid+1,r);
        return root;

    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return build(nums,0,nums.size()-1);
    }
};

把二叉搜索树转换为累加树

题目

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。节点的右子树仅包含键大于节点键的节点。左右子树也必须是二叉搜索树。注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1：

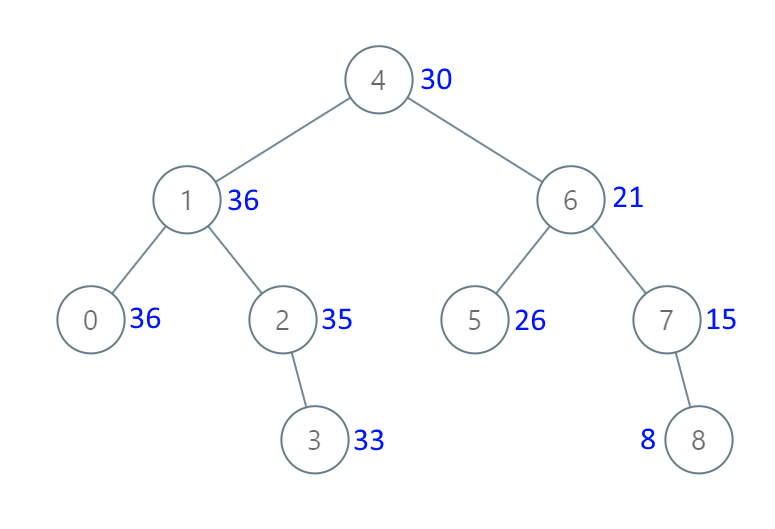
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8] 示例 2：

输入：root = [0,null,1] 输出：[1,null,1] 示例 3：

输入：root = [1,0,2] 输出：[3,3,2] 示例 4：

输入：root = [3,2,4,1] 输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 10^4 之间。每个节点的值介于 -10^4 和 10^4 之间。树中的所有值互不相同。给定的树为二叉搜索树。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/convert-bst-to-greater-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

递归

倒中序遍历后求前缀和

中序遍历是左-根-右

所以这里要右-根-左

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int cur = 0;
    TreeNode* convertBST(TreeNode* root) {
        if(root==nullptr) return root;
        convertBST(root->right);
        cur = cur + root->val;
        root->val = cur;
        convertBST(root->left);
        return root;
    }
};