二叉树（一）

前言

树的递归思维

这儿贴一下树，自顶向下和自底向上递归思维的差别。

树的自顶向下递归其实就是前序遍历，自底向上递归是后续遍历。

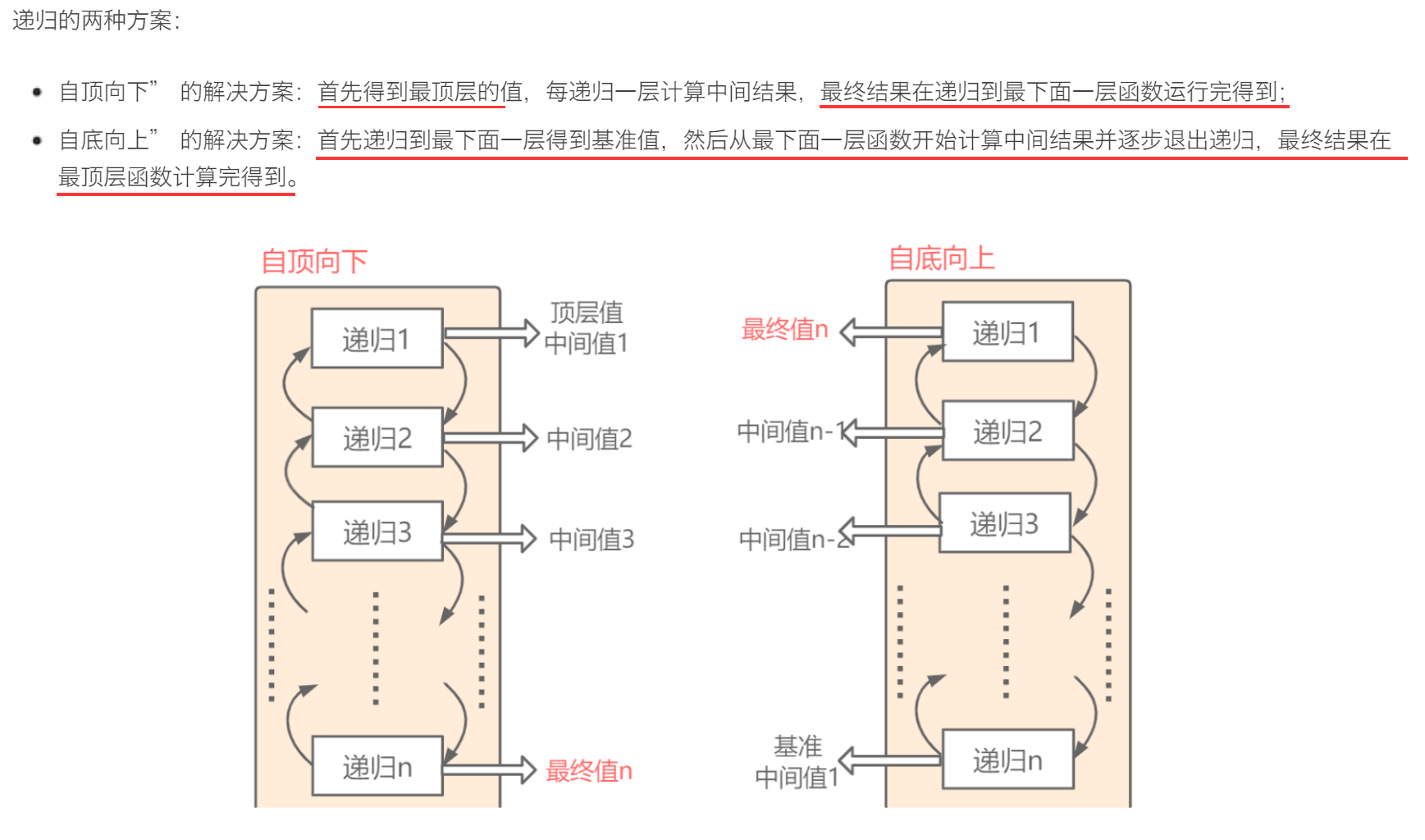
自顶向下（前序遍历）：确定一些参数，从该节点自身解决出发寻找答案；使用这些参数和节点本身的值来决定什么应该是传递给它子节点的参数

自底向上（后序遍历）：对于树中的任意一个节点，如果知道它子节点的答案，计算该节点的答案

二叉树的前序遍历

题目

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

输入：root = [1,null,2,3] 输出：[1,2,3]

示例 2：

输入：root = [] 输出：[]

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/binary-tree-preorder-traversal 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

递归解法

根节点——左子树——右子树

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void traversal(TreeNode* root, vector<int>& vec){
        if(root==nullptr) return;
        vec.push_back(root->val);
        traversal(root->left,vec);
        traversal(root->right,vec);

    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        traversal(root,res);
        return res;
    }
};

迭代解法

显式地利用栈来模拟递归，栈是先进先出的，为了先左后右，应该先加右节点再加左节点

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> stk;
        vector<int> res;
        if(!root) return res;

        stk.push(root);

        while(!stk.empty()){
            TreeNode* cur = stk.top();
            stk.pop();
            res.push_back(cur->val);
            if(cur->right) stk.push(cur->right);
            if(cur->left) stk.push(cur->left);
        }
        return res;
    }
};

在迭代的过程中，有两个操作，一个是处理操作即将元素放进result数组，另一个操作是访问操作，也就是遍历节点。

上面的的代码中处理和访问的顺序都是根左右

牢记前序遍历：先根节点，再左子树的根节点，再左左子树的根节点，…，再最左子节点的右子树..

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root==nullptr) return res;
        stack<TreeNode*> stk;
        TreeNode* node = root;
        while(stk.size() || node!=nullptr){
            while(node!=nullptr){
                res.push_back(node->val);
                stk.push(node);
                node = node->left;
            }
            node = stk.top();
            stk.pop();
            node = node->right;
        }
        return res;
    }
};

二叉树的中序遍历

题目

给定一个二叉树的根节点 root ，返回它的中序遍历。

示例 1：

输入：root = [1,null,2,3] 输出：[1,3,2] 示例 2：

输入：root = [] 输出：[] 示例 3：

输入：root = [1] 输出：[1]

提示：

树中节点数目在范围 [0, 100] 内 -100 <= Node.val <= 100

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/binary-tree-inorder-traversal 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

递归解法

左子树——根节点——右子树

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void inorder(TreeNode* root, vector<int>& res){
        if(!root) return;
        inorder(root->left,res);
        res.push_back(root->val);
        inorder(root->right,res);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        inorder(root,ans);
        return ans;
    }
};

迭代解法

中序遍历是左根右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

下面这种写法和前序遍历的区别就是访问的顺序一样，处理的顺序不一样

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root==nullptr) return res;
        stack<TreeNode*> stk;
        TreeNode* node = root;
        while(!stk.empty() || node!=nullptr){
            while(node!=nullptr){
                stk.push(node);
                node = node->left;
            }
            node = stk.top();
            stk.pop();
            res.push_back(node->val);//先左 再根
            node = node->right;//最后右
        }
        return res;
    }
};

二叉树的后序遍历

题目

给你一棵二叉树的根节点 root ，返回其节点值的后序遍历。

示例 1：

输入：root = [1,null,2,3] 输出：[3,2,1] 示例 2：

输入：root = [] 输出：[] 示例 3：

输入：root = [1] 输出：[1]

提示：

树中节点的数目在范围 [0, 100] 内 -100 <= Node.val <= 100

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/binary-tree-postorder-traversal 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

递归解法

左子树——右子树——根节点

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
public:
    void postorder(TreeNode *root, vector<int> &res) {
        if (root == nullptr) {
            return;
        }
        postorder(root->left, res);
        postorder(root->right, res);
        res.push_back(root->val);
    }

    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> ans;
        postorder(root, ans);
        return ans;
    }
};

迭代解法

与中序的不同之处在于：
中序遍历中，从栈中弹出的节点，其左子树是访问完了，可以直接访问该节点，然后接下来访问右子树。
后序遍历中，从栈中弹出的节点，我们只能确定其左子树肯定访问完了，但是无法确定右子树是否访问过。
因此，我们在后序遍历中，引入了一个prev来记录历史访问记录。
当访问完一棵子树的时候，我们用prev指向该节点。
这样，在回溯到父节点的时候，我们可以依据prev是指向左子节点，还是右子节点，来判断父节点的访问情况。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root==nullptr) return res;
        stack<TreeNode*> stk;
        TreeNode *node = root, *prev = nullptr;
        while(!stk.empty() || node!=nullptr){
            while(node!=nullptr){
                stk.push(node);
                node = node->left;
            }
            node = stk.top();
            stk.pop();
            if(node->right == nullptr || node->right == prev){//无右子树 或 右子树访问完
                res.push_back(node->val);
                prev = node;
                node = nullptr;
            }else{
                //否则将其重新压栈，开始访问右子树
                stk.push(node);
                node = node->right;
            }
        }

        return res;
    }
};

还有一种解法是根据前序遍历的迭代解法修改得来的：

前序：根左右后序：左右根

在前序遍历的第一种迭代解法中，改变一下左右的顺序，可以得到根右左的遍历，此时将这个遍历翻转一下便可得到左右根

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node->right) st.push(node->right); // 空节点不入栈
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};

二叉树的层次遍历

题目

给你二叉树的根节点 root ，返回其节点值的层序遍历。（即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7] 输出：[[3],[9,20],[15,7]] 示例 2：

输入：root = [1] 输出：[[1]] 示例 3：

输入：root = [] 输出：[]

提示：

树中节点数目在范围 [0, 2000] 内 -1000 <= Node.val <= 1000

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/binary-tree-level-order-traversal 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

迭代解法（BFS）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        vector<vector<int>> res;
        if(!root) return res;
        que.push(root);
        while(!que.empty()){
            vector<int> level;
            int q = que.size();
            while(q--){//一次将队列中的所有元素都取出来
                TreeNode* node = que.front();
                que.pop();
                level.push_back(node->val);
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            res.push_back(level);
        }
        return res;
    }
};

递归解法

在递归函数多加一个表示层级的参数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> res;
    vector<int> empty;
    void dfs(TreeNode* root, int level){
        if(!root) return;
        if(level>=res.size()){
            res.push_back(empty);
        }
        res[level].push_back(root->val);
        dfs(root->left,level+1);
        dfs(root->right,level+1);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        if(!root) return res;
        res.push_back(empty);
        dfs(root, 0);
        return res;
    }
};

判断是否为平衡二叉树

题目

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

输入：root = [3,9,20,null,null,15,7] 输出：true 示例 2：

输入：root = [1,2,2,3,3,null,null,4,4] 输出：false 示例 3：

输入：root = [] 输出：true

提示：

树中的节点数在范围 [0, 5000] 内 -104 <= Node.val <= 104

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/balanced-binary-tree 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

自顶向下的递归

先定义一个计算高度的函数，用于计算二叉树中的任一节点的高度。然后即可判断二叉树是否平衡。

具体做法类似于二叉树的前序遍历，即对于当前遍历到的节点，首先计算左右子树的高度，如果左右子树的高度差是否不超过 1，再分别递归地遍历左右子节点，并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    
    int getHeight(TreeNode* root){
        if(root==nullptr) return 0;
        int res = 1+max(getHeight(root->left),getHeight(root->right));
        return res;
    }
    bool isBalanced(TreeNode* root) {
        if(root==nullptr) return true;
        int heightdiff = abs(getHeight(root->left)-getHeight(root->right));
        return heightdiff<=1 && isBalanced(root->left) && isBalanced(root->right);
    }
};

注意到上面这种方法有大量的重复计算，越下层节点调用getHeight次数越多。

可以加上备忘录。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<TreeNode*, int> height;//记忆化
    int getHeight(TreeNode* root){
        if(root==nullptr) return 0;
        if(height.count(root)) return height[root];
        int res = 1+max(getHeight(root->left),getHeight(root->right));
        height.emplace(root,res);
        return res;
    }
    bool isBalanced(TreeNode* root) {
        if(root==nullptr) return true;
        int heightdiff = abs(getHeight(root->left)-getHeight(root->right));
        return heightdiff<=1 && isBalanced(root->left) && isBalanced(root->right);
    }
};

自底向上的递归

自底向上递归的做法类似于后序遍历，对于当前遍历到的节点，先递归地判断其左右子树是否平衡，再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的，则返回其高度（高度一定是非负整数），否则返回 -1。如果存在一棵子树不平衡，则整个二叉树一定不平衡。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int height(TreeNode* root) {
        if (root == NULL) {
            return 0;
        }
        int leftHeight = height(root->left);
        int rightHeight = height(root->right);
        if (leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1) {
            return -1;
        } else {
            return max(leftHeight, rightHeight) + 1;
        }
    }

    bool isBalanced(TreeNode* root) {
        return height(root) >= 0;
    }
};

二叉树上的路径总和

题目

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出：true 解释：等于目标和的根节点到叶节点路径如上图所示。示例 2：

输入：root = [1,2,3], targetSum = 5 输出：false 解释：树中存在两条根节点到叶子节点的路径： (1 –> 2): 和为 3 (1 –> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。示例 3：

输入：root = [], targetSum = 0 输出：false 解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内 -1000 <= Node.val <= 1000 -1000 <= targetSum <= 1000

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/path-sum 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路及代码

dfs(node,sum)：是否存在从节点node到某个叶子节点的路径和为sum

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool dfs(TreeNode *node , int sum){
        if(node == nullptr) return false;
        if(node->left==nullptr && node->right==nullptr && sum - node->val == 0) return true;
        
        int restsum = sum - node->val;
        // cout<<"val: "<<node->val<<' '<<"sum: "<<restsum<<endl;
        if(dfs(node->left, restsum)) return true;

        if(dfs(node->right, restsum)) return true;

        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        return dfs(root,targetSum);
    }   
};

二叉树上的路径总和II

题目

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。

叶子节点是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出：[[5,4,11,2],[5,8,4,5]] 示例 2：

输入：root = [1,2,3], targetSum = 5 输出：[] 示例 3：

输入：root = [1,2], targetSum = 0 输出：[]

提示：

树中节点总数在范围 [0, 5000] 内 -1000 <= Node.val <= 1000 -1000 <= targetSum <= 1000

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/path-sum-ii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路及代码

采用深度优先搜索的方式，枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点，且此时路径和恰为目标和时，我们就找到了一条满足条件的路径。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;

    void dfs(TreeNode* root, int targetSum) {
        if (root == nullptr) {
            return;
        }
        path.emplace_back(root->val);
        targetSum -= root->val;
        if (root->left == nullptr && root->right == nullptr && targetSum == 0) {
            ret.emplace_back(path);
        }
        dfs(root->left, targetSum);
        // path.pop_back();
        // path.push_back(root->val);  //这两步相当于啥都没干，所以可以省略
        dfs(root->right, targetSum);
        path.pop_back();
    }

    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        dfs(root, targetSum);
        return ret;
    }
};

二叉树上的路径总和III

题目

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出：3 解释：和等于 8 的路径有 3 条，如图所示。示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出：3

提示:

二叉树的节点个数的范围是 [0,1000] -109 <= Node.val <= 109 -1000 <= targetSum <= 1000

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/path-sum-iii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

嵌套DFS

和前两题不同的是，这里的路径不要求是根节点到叶子节点。

函数rootSum(root,targetSum)求以root节点为根的路径总和为targetSum的路径数

函数pathSum(root,targetSum)求根节点是root的树中路径总和为targetSum的路径数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int rootSum(TreeNode* root, int targetSum) {
        if (!root) {
            return 0;
        }
        int ret = 0;
        if (root->val == targetSum) {
            ret++;
        } 
        ret += rootSum(root->left, targetSum - root->val);
        ret += rootSum(root->right, targetSum - root->val);
        return ret;
    }
    int pathSum(TreeNode* root, int targetSum) {
        if (!root) {
            return 0;
        }
        int ret = rootSum(root, targetSum);
        ret += pathSum(root->left, targetSum);
        ret += pathSum(root->right, targetSum);
        return ret;
    }
};

前缀和

记当前节点为cur，那么前缀和为当前节点到根节点路径的路径和

如果下一节点next的前缀和减去当前节点cur的前缀和等于 target，那么就说明cur->val = target

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, int> table;//table[i][j] -> 前缀和为i的有j个
    int ans = 0;
    void dfs(TreeNode* node, int curPrefix, int targetSum){
        if(node == nullptr) return;
        curPrefix = curPrefix + node->val;
        if(table.count(curPrefix-targetSum)) ans+=table[curPrefix-targetSum];

        table[curPrefix]++;
        dfs(node->left,curPrefix,targetSum);
        //想象一下平常循环里的回溯
        dfs(node->right,curPrefix,targetSum);
        table[curPrefix]--;//回溯，这个是全局变量，退出当前层必须要回溯即清空当前层对该全局变量的影响
    }
    int pathSum(TreeNode* root, int targetSum) {
        table[0] = 1;
        if(root == nullptr) return 0;
        dfs(root,0,targetSum);
        return ans;
    }
};