差分

# 引言

差分是一种和前缀和相对的策略，可以当作是求和的逆运算 $$ \begin{equation} b_i= \begin{cases} a_i-a_{i-1} , & i\in[2,n] \ a_1 , & i = 1 \end{cases} \end{equation} $$ 简单性质：

1）计算数列各项的值。 $$ \begin{equation} a[n] = \sum_{i=1}^{n} b[i] \end{equation} $$ 2）计算数列的前缀和。 $$ \begin{equation} sum_n = \sum_{i=1}^{n}a_i = \sum_{i=1}^{n}\sum_{j=1}^{i}b_j = \sum_{i=1}^{n}(n-i+1)b_i \end{equation} $$ 用途：

维护多次对数列的一个区间加上一个数，并在最后询问某一位的数或多次询问某一位的数

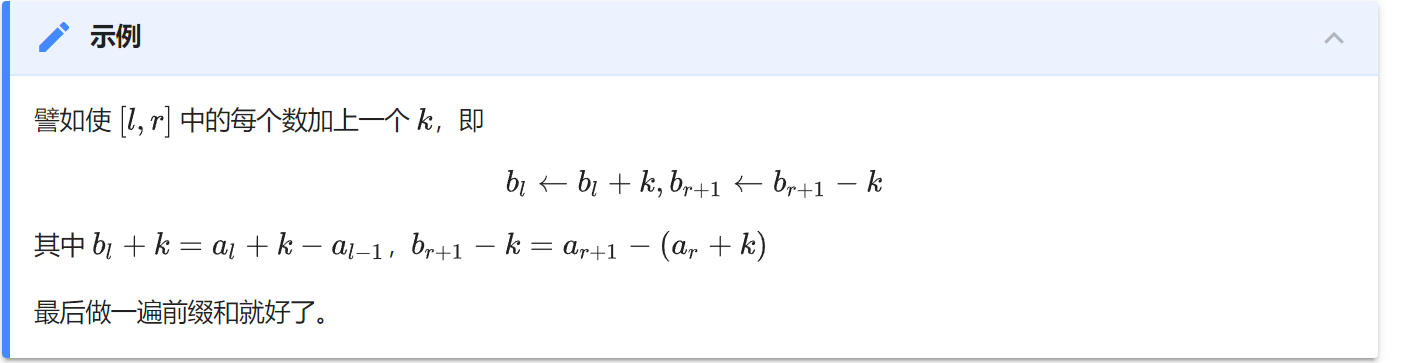
$b_l+k$可看成[l,n]的变化量加k，这也导致了r后面也加了k，所以还要令$b_{r+1}-k$，表示[r+1,n]的变化量减k

# 航班预定统计

# 题目

这里有 n 个航班，它们分别从 1 到 n 进行编号。

有一份航班预订表 bookings ，表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti （包含 firsti 和 lasti ）的每个航班上预订了 seatsi 个座位。

请你返回一个长度为 n 的数组 answer，里面的元素是每个航班预定的座位总数。

示例 1：

输入：bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5 输出：[10,55,45,25,25] 解释：航班编号 1 2 3 4 5 预订记录 1 ： 10 10 预订记录 2 ： 20 20 预订记录 3 ： 25 25 25 25 总座位数： 10 55 45 25 25 因此，answer = [10,55,45,25,25] 示例 2：

输入：bookings = [[1,2,10],[2,2,15]], n = 2 输出：[10,25] 解释：航班编号 1 2 预订记录 1 ： 10 10 预订记录 2 ： 15 总座位数： 10 25 因此，answer = [10,25]

提示：

1 <= n <= 2 * 10^4

1 <= bookings.length <= 2 * 10^4

bookings[i].length == 3

1 <= firsti <= lasti <= n

1 <= seatsi <= 10^4

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/corporate-flight-bookings 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

# 解题思路

区间修改单点查询

差分模板题

# 代码

注意编号，题中的航班编号从1开始

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
        vector<int> diff(n+2);
        for(auto &book: bookings){
            diff[book[0]] += book[2];
            diff[book[1]+1] -= book[2];
        }
        int now = 0;
        vector<int> res;
        for(int i=1;i<=n;i++){
            now += diff[i];
            res.push_back(now);
        }
        return res;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
public:
    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
        vector<int> nums(n);
        for (auto& booking : bookings) {
            nums[booking[0] - 1] += booking[2];
            if (booking[1] < n) {
                nums[booking[1]] -= booking[2];
            }
        }
        for (int i = 1; i < n; i++) {
            nums[i] += nums[i - 1];
        }
        return nums;
    }
};

# 拼车

# 题目

车上最初有 capacity 个空座位。车只能向一个方向行驶（也就是说，不允许掉头或改变方向）

给定整数 capacity 和一个数组 trips , trip[i] = [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客，接他们和放他们的位置分别是 fromi 和 toi 。这些位置是从汽车的初始位置向东的公里数。

当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false。

示例 1：

输入：trips = [[2,1,5],[3,3,7]], capacity = 4 输出：false 示例 2：

输入：trips = [[2,1,5],[3,3,7]], capacity = 5 输出：true

提示：

1 <= trips.length <= 1000

trips[i].length == 3

1 <= numPassengersi <= 100

0 <= fromi < toi <= 1000

1 <= capacity <= 10^5

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/car-pooling 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

# 解题思路

区间修改单点查询

这题和上一题有点不一样，如果同一距离有人上车也有人下车，是假设下车完再上车的，

也就是说对差分数组diff，diff[start] += k 不变，start地点开始上车，而diff[end] -= k（不是diff[end+1]-=k），表示end地点都可下车完。

再判断每一单点距离是否超载

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        map<int,int> tab;
        int far = 0;
        for(auto &x:trips){
            tab[x[1]]+=x[0];
            tab[x[2]]-=x[0];
            far = max(far,x[2]);
        }
        int cur=0;
        for(int i=0;i<=far;i++){
            cur += tab[i];
            if(cur>capacity) return false;
        }
        return true;
    }
};

# 我的日程安排表 II

# 题目

实现一个 MyCalendar 类来存放你的日程安排。如果要添加的时间内不会导致三重预订时，则可以存储这个新的日程安排。

MyCalendar 有一个 book(int start, int end)方法。它意味着在 start 到 end 时间内增加一个日程安排，注意，这里的时间是半开区间，即 [start, end), 实数 x 的范围为， start <= x < end。

当三个日程安排有一些时间上的交叉时（例如三个日程安排都在同一时间内），就会产生三重预订。

每次调用 MyCalendar.book方法时，如果可以将日程安排成功添加到日历中而不会导致三重预订，返回 true。否则，返回 false 并且不要将该日程安排添加到日历中。

请按照以下步骤调用MyCalendar 类: MyCalendar cal = new MyCalendar(); MyCalendar.book(start, end)

示例：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
MyCalendar();
MyCalendar.book(10, 20); // returns true
MyCalendar.book(50, 60); // returns true
MyCalendar.book(10, 40); // returns true
MyCalendar.book(5, 15); // returns false
MyCalendar.book(5, 10); // returns true
MyCalendar.book(25, 55); // returns true
解释： 
前两个日程安排可以添加至日历中。 第三个日程安排会导致双重预订，但可以添加至日历中。
第四个日程安排活动（5,15）不能添加至日历中，因为它会导致三重预订。
第五个日程安排（5,10）可以添加至日历中，因为它未使用已经双重预订的时间10。
第六个日程安排（25,55）可以添加至日历中，因为时间 [25,40] 将和第三个日程安排双重预订；
时间 [40,50] 将单独预订，时间 [50,55）将和第二个日程安排双重预订。

提示：

每个测试用例，调用 MyCalendar.book 函数最多不超过 1000次。调用函数 MyCalendar.book(start, end)时， start 和 end 的取值范围为 [0, 10^9]。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/my-calendar-ii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

# 解题思路

区间修改单点查询

还是可以用差分数组的思想

注意数据范围，时间的数据范围达到了10^9，如果用int保存完整的差分数组的话空间会炸

但是调用book函数最多不超过1000次。

所以可以直接用map存储差分数组，只存储改变后的值即可

diff[start]++ 表示时间start后（含）预定数会加1

diff[end]– 表示时间end后（含）预定数会减1，这样累加后只有[start, end)区间的预定数会加1

累加时只需累加到end，并且只需要在每个时间点有变化量的时候更新即可，在这个过程中判断是否出现大于两次的预定

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class MyCalendarTwo {
private:
    map<int,int> diff;
public:
    MyCalendarTwo() {
        diff.clear();
    }
    
    bool book(int start, int end) {
        diff[start]++,diff[end]--;
        int now=0;
        for(auto &x:diff){
            if(x.first >= end) break;
            now += x.second;
            if(now > 2){//出现三重预定，复原并返回false
                diff[start]--;
                diff[end]++;
                return false;
            }
        }
        return true;
    }
};

/**
 * Your MyCalendarTwo object will be instantiated and called as such:
 * MyCalendarTwo* obj = new MyCalendarTwo();
 * bool param_1 = obj->book(start,end);
 */

# K连续位的最小翻转次数

# 题目

给定一个二进制数组 nums 和一个整数 k 。

k位翻转就是从 nums 中选择一个长度为 k 的子数组，同时把子数组中的每一个 0 都改成 1 ，把子数组中的每一个 1 都改成 0 。

返回数组中不存在 0 所需的最小 k位翻转次数。如果不可能，则返回 -1 。

子数组是数组的连续部分。

示例 1：

输入：nums = [0,1,0], K = 1 输出：2 解释：先翻转 A[0]，然后翻转 A[2]。示例 2：

输入：nums = [1,1,0], K = 2 输出：-1 解释：无论我们怎样翻转大小为 2 的子数组，我们都不能使数组变为 [1,1,1]。示例 3：

输入：nums = [0,0,0,1,0,1,1,0], K = 3 输出：3 解释：翻转 A[0],A[1],A[2]: A变成 [1,1,1,1,0,1,1,0] 翻转 A[4],A[5],A[6]: A变成 [1,1,1,1,1,0,0,0] 翻转 A[5],A[6],A[7]: A变成 [1,1,1,1,1,1,1,1]

提示：

1 <= nums.length <= 10^5 1 <= k <= nums.length

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/minimum-number-of-k-consecutive-bit-flips 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

# 解题思路

首先是如何翻转，考虑贪心，每次找到第一个0的位置，以该位置为起点连续K个数进行翻转。可以举举例子，论证这样翻转是正确的。

然后就涉及到了区间修改问题，注意数据规模，显然不能用O(n)的时间进行翻转。

考虑用差分思想，进行区间修改。

假设位置i的数为0，那么需要对区间[i,i+k)的数进行翻转，如果i+k大于数组长度（边界为i+k-1==len-1）说明剩下的数不能全部翻转为1了

对区间[i,i+k）进行修改（加1即可，最后模2判断是否为0），令差分数组d[i]++, d[i+k]–，这就完成了区间修改操作

接下来需要进行单点查询操作，注意细节，因为是边修改边查询

注意区间更新后，变化量也要及时更新

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
const int MAXN = 1e5+5;

class Solution {
public:

    int minKBitFlips(vector<int>& nums, int k) {
        int len = nums.size();
        int res = 0,now = 0;
        vector<int> diff(len+5,0);//差分数组
        for(int i=0;i<len;i++){
            now += diff[i];//累加变化量
            // cout<<"i: "<<i<<" a[i]: "<<(nums[i]+now)%2<<endl;
            if((nums[i] + now)%2 == 0){
                int r = i+k;
                if(r>len){
                    res = -1;
                    break;
                }
                
                diff[i]++;
                diff[r]--;//[i,r) +1
                now++;//i处的变化量发生变化了，记得加上新的变化
                res ++;//翻转次数加1
            }
            
        }
        return res;
    }
};

or：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
const int MAXN = 1e5+5;

class Solution {
public:

    int minKBitFlips(vector<int>& nums, int k) {
        int len = nums.size();
        int res = 0,now = 0;
        vector<int> diff(len+5,0);//差分数组
        for(int i=0;i<len;i++){
            now += diff[i];//累加变化量
            // cout<<"i: "<<i<<" a[i]: "<<(nums[i]+now)%2<<endl;
            if((nums[i] + now)%2 == 0){
                int r = i+k;
                if(r>len){
                    res = -1;
                    break;
                }
                diff[i+1]++;
                diff[r]--;//[i+1,r) +1，默认i处已翻转完成
                res ++;//翻转次数加1
            }
            
        }
        return res;
    }
};