引言
树型DP求树的直径——CSDN
树的直径——CSDN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| //树形dp解树的直径的两种写法:
//第一种写法
int vis[N];
int res=INT_MIN; //初始为一个很小的值
int d[N],f[N];//d[u]为节点u到其子孙节点的最长路径 f[u]为u为根节点时最长路径和(u的最长+u的次长)
void dfs(int u){
vis[u]=1;
//遍历u的出边
for(int i=head[u];i>=0;i=e[i].next){
int v=e[i].v;
int w=e[i].w;
if(!vis[v]){ //如果是u的子节点
dfs(v);//计算子节点的信息
/*一定是先计算f[u]再计算d[u]的
如果先计算d[u]的话,f[u]就会计算 最长路径+最长路径,也就是说会重复计算最长路径
边权可能为负的情况*/
f[u]=max(max(f[u],d[u]),max(d[v]+w,d[u]+d[v]+w));
d[u]=max(max(d[u],w),d[v]+w);
}
}
}
dfs(1);
for(int i=1;i<=n;i++) res=max(res,f[i]);
printf("%d\n",res);
//第二种写法:
int vis[N];
int res=INT_MIN;
int dfs(int u){//dfs(u) 计算d[u]的值
vis[u]=1;
int ud=0;
for(int i=head[u];i>=0;i=e[i].next){
int v=e[i].v;
int w=e[i].w;
if(!vis[v]){
int vd=dfs(v);//计算d[v]
//原res值
//ud>=0 ,最长路径 , 避免次长路径为负
//vd+w, 次长路径,避免ud未赋值时情况
//ud+vd+w,最长路径+次长路径
res=max(max(res,ud),max(vd+w,ud+vd+w));
//原ud值
//w,避免子孙为负
//vd+w,vd>=0,加上w
ud=max(max(ud,w),vd+w);
}
}
return ud;
}
|
二叉树的直径
题目
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/diameter-of-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
路径长度改成路径上边的数目
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int res;
int dfs(TreeNode* root){//root到其子孙节点最大路径节点个数
if(root == nullptr) return 0;
int t1 = 0, t2 = 0;//最长,次长
t1 = dfs(root->left);
t2 = dfs(root->right);
if(t1<t2) swap(t1,t2);//确保t1>t2
res = max(res,t1+t2+1);//
return t1+1;//一条边的权值为1
}
int diameterOfBinaryTree(TreeNode* root) {
dfs(root);
return res-1;//节点个数-1为路径长度
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
private:
int res=INT_MIN;
public:
int dfs(TreeNode* root){
if(root==nullptr) return 0;
int d=0;
int l=dfs(root->left);
int r=dfs(root->right);
d=max(l+1,r+1);
res=max(res,l+r);
return d;
}
int diameterOfBinaryTree(TreeNode* root) {
dfs(root);
return res;
}
};
|
二叉树的最大路径和
题目
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
输入:root = [1,2,3]
输出:6
解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
树中节点数目范围是 [1, 3 * 10^4]
-1000 <= Node.val <= 1000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-maximum-path-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
模板题中的路径和是路径上边的权值,而此处是路径上点的权值。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int res=-3e7;
int dfs(TreeNode* root){//root到其子孙节点的最大路径和
if(root == nullptr) return 0;
int maxd = -3e7;//当前root到子孙节点的最大路径和
int dL = dfs(root->left);
//原res,最大路径,次大路径,最大+次大
res = max(max(res,maxd),max(dL+root->val,maxd+dL));
maxd = max(maxd,max(root->val,dL+root->val));
int dR = dfs(root->right);
res = max(max(res,maxd),max(dR+root->val,maxd+dR));
maxd = max(maxd,max(root->val,dR+root->val));
return maxd;
}
int maxPathSum(TreeNode* root) {
dfs(root);
return res;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int res=INT_MIN;
public:
int dfs(TreeNode *root){
if(root==nullptr) return 0;
int d=root->val;
int l=dfs(root->left);
int r=dfs(root->right);
res=max(max(res,d+l+r),max(d,max(d+r,d+l)));
d=max(d,max(d+l,d+r));
return d; //返回 以当前节点为根的到达子孙节点的最长路径和
}
int maxPathSum(TreeNode* root) {
dfs(root);
return res;
}
};
|
如果不用上述思想:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
private:
int maxSum = INT_MIN;
public:
int maxGain(TreeNode* node) {
if (node == nullptr) {
return 0;
}
// 递归计算左右子节点的最大贡献值
// 只有在最大贡献值大于 0 时,才会选取对应子节点
int leftGain = max(maxGain(node->left), 0);
int rightGain = max(maxGain(node->right), 0);
// 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
int priceNewpath = node->val + leftGain + rightGain;
// 更新答案
maxSum = max(maxSum, priceNewpath);
// 返回节点的最大贡献值
return node->val + max(leftGain, rightGain);
}
int maxPathSum(TreeNode* root) {
maxGain(root);
return maxSum;
}
};
|
最长同值路径
题目
给定一个二叉树的 root ,返回 最长的路径的长度 ,这个路径中的 每个节点具有相同值 。 这条路径可以经过也可以不经过根节点。
两个节点之间的路径长度 由它们之间的边数表示。
示例 1:
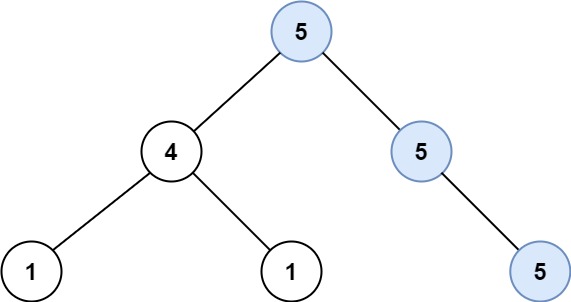
输入:root = [5,4,5,1,1,5]
输出:2
示例 2:
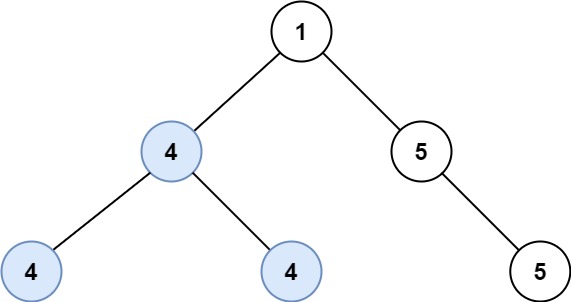
输入:root = [1,4,5,4,4,5]
输出:2
提示:
树的节点数的范围是 [0, 10^4]
-1000 <= Node.val <= 1000
树的深度将不超过 1000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-univalue-path
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
最长路径长度加了个同值的条件
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int res = 1;
int dfs(TreeNode* u){//u到子孙节点的最长同值路径节点个数
int t1 = 0, t2 = 0;//最长 次长
if(u->left){
if(u->left->val == u->val){//同值情况,更新答案
int dv = dfs(u->left);
if(dv>t1) t2=t1,t1=dv;
else if(dv>t2) t2=dv;
res = max(res,t1+t2+1);
}else{
dfs(u->left);
}
}
if(u->right){
if(u->right->val == u->val){
int dv = dfs(u->right);
if(dv>t1) t2=t1,t1=dv;
else if(dv>t2) t2=dv;
res = max(res,t1+t2+1);
}else{
dfs(u->right);
}
}
return t1+1;
}
int longestUnivaluePath(TreeNode* root) {
if(root == nullptr) return 0;
dfs(root);
return res-1;//节点个数-1为路径长度
}
};
|
相邻字符不同的最长路径
题目
给你一棵 树(即一个连通、无向、无环图),根节点是节点 0 ,这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树,其中 parent[i] 是节点 i 的父节点,由于节点 0 是根节点,所以 parent[0] == -1 。
另给你一个字符串 s ,长度也是 n ,其中 s[i] 表示分配给节点 i 的字符。
请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ,并返回该路径的长度。
示例 1:

1
2
3
4
| 输入:parent = [-1,0,0,1,1,2], s = "abacbe"
输出:3
解释:任意一对相邻节点字符都不同的最长路径是:0 -> 1 -> 3 。该路径的长度是 3 ,所以返回 3 。
可以证明不存在满足上述条件且比 3 更长的路径。
|
示例 2:

1
2
3
| 输入:parent = [-1,0,0,0], s = "aabc"
输出:3
解释:任意一对相邻节点字符都不同的最长路径是:2 -> 0 -> 3 。该路径的长度为 3 ,所以返回 3 。
|
提示:
n == parent.length == s.length1 <= n <= 105- 对所有
i >= 1 ,0 <= parent[i] <= n - 1 均成立 parent[0] == -1parent 表示一棵有效的树s 仅由小写英文字母组成
解题思路
289场周赛第4题
求最长路径,但相邻两节点字符不同
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
vector<vector<int>> G;//邻接矩阵
string s;
int res;
int dfs(int u){//节点u到其子孙节点合法的最长距离
int t1=0,t2=0;//子节点到其子孙节点合法的最长距离、子节点到其子孙节点合法的次长距离
for(auto v:G[u]){//遍历子节点
if(s[v] == s[u]){//相邻字符相同 即子节点与父亲节点字符相同
dfs(v);//求子节点到其子孙节点合法的最长距离
}else{
int cur = dfs(v);
if(cur>t1) t2 = t1, t1 = cur;//更新最大值
else if(cur>t2) t2 = cur;//更新次大值
}
}
res = max(res,t1+t2+1);//以u为根节点的最长路径:最长+次长+1
return t1+1;//加上本身的1
}
int longestPath(vector<int>& parent, string s) {
G.resize(parent.size());
this->s = s;
for(int i=1;i<parent.size();i++)
G[parent[i]].push_back(i);//建图
dfs(0);//从根节点出发
return res;
}
};
|




