Featured image of post LeetCode第290场周赛总结
leetcode contest

LeetCode第290场周赛总结

1790/6275

image-20220424130334022

# 【模拟】多个数组求交集

# 题目

给你一个二维整数数组 nums ，其中 nums[i] 是由 不同 正整数组成的一个非空数组，按 升序排列 返回一个数组，数组中的每个元素在 nums 所有数组 中都出现过。

示例 1：

1
2
3
4

输入：nums = [[3,1,2,4,5],[1,2,3,4],[3,4,5,6]]
输出：[3,4]
解释：
nums[0] = [3,1,2,4,5]，nums[1] = [1,2,3,4]，nums[2] = [3,4,5,6]，在 nums 中每个数组中都出现的数字是 3 和 4 ，所以返回 [3,4] 。

示例 2：

1
2
3
4

输入：nums = [[1,2,3],[4,5,6]]
输出：[]
解释：
不存在同时出现在 nums[0] 和 nums[1] 的整数，所以返回一个空列表 [] 。

提示：

  • 1 <= nums.length <= 1000
  • 1 <= sum(nums[i].length) <= 1000
  • 1 <= nums[i][j] <= 1000
  • nums[i] 中的所有值 互不相同

# 解题思路

定义一个map，统计每个数出现的次数，最后判断是否为n即可

map会自动排序

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
public:
    vector<int> intersection(vector<vector<int>>& nums) {
        int n = nums.size();
        
        map<int,int> tab;
        
        for(auto &x: nums){
            for(auto y:x){
                tab[y]++;
            }
        }
        
        vector<int> res;
        for(auto &x: tab){
            if(x.second == n){
                res.push_back(x.first);
            }
        }
        
        return res; 
    }
};

# 【枚举】统计圆内格点数目

# 题目

给你一个二维整数数组 circles ，其中 circles[i] = [xi, yi, ri] 表示网格上圆心为 (xi, yi) 且半径为 ri 的第 i 个圆，返回出现在 至少一个 圆内的 格点数目 。

注意：

  • 格点 是指整数坐标对应的点。
  • 圆周上的点 也被视为出现在圆内的点。

示例 1：

1
2
3
4
5
6
7

输入：circles = [[2,2,1]]
输出：5
解释：
给定的圆如上图所示。
出现在圆内的格点为 (1, 2)、(2, 1)、(2, 2)、(2, 3) 和 (3, 2)，在图中用绿色标识。
像 (1, 1) 和 (1, 3) 这样用红色标识的点，并未出现在圆内。
因此，出现在至少一个圆内的格点数目是 5 。

示例 2：

1
2
3
4
5
6

输入：circles = [[2,2,2],[3,4,1]]
输出：16
解释：
给定的圆如上图所示。
共有 16 个格点出现在至少一个圆内。
其中部分点的坐标是 (0, 2)、(2, 0)、(2, 4)、(3, 2) 和 (4, 4) 。

提示：

  • 1 <= circles.length <= 200
  • circles[i].length == 3
  • 1 <= xi, yi <= 100
  • 1 <= ri <= min(xi, yi)

# 解题思路

很难受啊，这题TLE了一发

看数据规模是妥妥的暴力，没想到竟然TLE了，一开始是枚举200*200个点，再在最多200个圆里判断是否出现在其中，TLE了

然后换了个遍历的思路，先枚举圆，再统计该圆覆盖的格点数目，最后再统计200*200个格点，看出现次数是否大于0，A了

结束后，发现其实两种思路都能过的，毕竟数据范围就10^6，第一次TLE的原因是auto没加引用

也就是说，以后用auto，能加引用就加，速度会快一点

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

#define P pair<int,int>
class Solution {
public:
    bool isok(int x, int y, int r, P point){
        int dis = (point.first-x)*(point.first-x) + (point.second-y)*(point.second-y);
        return dis<=r*r;
    }
    int countLatticePoints(vector<vector<int>>& circles) {
        int res = 0;
        for(int xi = 0; xi <= 205; xi++){
            for(int yi = 0; yi<=205; yi++){
                for(auto &cir: circles){//原先没加引用，超时了，加了后就过了
                    if(isok(cir[0],cir[1],cir[2],P(xi,yi))){
                        res++;
                        break;
                    }
                }
            }
        }
        return res;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#define P pair<int,int>
class Solution {
public:
    bool isok(int x, int y, int r, P point){
        int dis = (point.first-x)*(point.first-x) + (point.second-y)*(point.second-y);
        return dis<=r*r;
    }
    int countLatticePoints(vector<vector<int>>& circles) {
        int res = 0;
        vector<vector<int>> have(205);
        for(int i=0;i<205;i++) have[i].resize(205,0);
        
        for(auto cir:circles){//以后加引用
            int x = cir[0],y=cir[1],r=cir[2];
            for(int i = x-r; i<=x+r;i++){
                for(int j = y-r;j<=y+r;j++){
                    if(isok(x,y,r,P(i,j))) have[i][j]++;
                }
            }
        }
        
        for(auto x:have){//以后加引用
            for(auto y:x){
                if(y) res++;
            }
        }
        
        return res;
    }
};

# 【枚举+二分】统计包含每个点的矩形数目

# 题目

给你一个二维整数数组 rectangles ，其中 rectangles[i] = [li, hi] 表示第 i 个矩形长为 li 高为 hi 。给你一个二维整数数组 points ，其中 points[j] = [xj, yj] 是坐标为 (xj, yj) 的一个点。

第 i 个矩形的 左下角 在 (0, 0) 处，右上角 在 (li, hi) 。

请你返回一个整数数组 count ，长度为 points.length，其中 count[j]是 包含 第 j 个点的矩形数目。

如果 0 <= xj <= li 且 0 <= yj <= hi ，那么我们说第 i 个矩形包含第 j 个点。如果一个点刚好在矩形的 边上 ，这个点也被视为被矩形包含。

示例 1：

1
2
3
4
5
6
7
8
9

输入：rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
输出：[2,1]
解释：
第一个矩形不包含任何点。
第二个矩形只包含一个点 (2, 1) 。
第三个矩形包含点 (2, 1) 和 (1, 4) 。
包含点 (2, 1) 的矩形数目为 2 。
包含点 (1, 4) 的矩形数目为 1 。
所以，我们返回 [2, 1] 。

示例 2：

1
2
3
4
5
6
7
8
9

输入：rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
输出：[1,3]
解释：
第一个矩形只包含点 (1, 1) 。
第二个矩形只包含点 (1, 1) 。
第三个矩形包含点 (1, 3) 和 (1, 1) 。
包含点 (1, 3) 的矩形数目为 1 。
包含点 (1, 1) 的矩形数目为 3 。
所以，我们返回 [1, 3] 。

提示：

  • 1 <= rectangles.length, points.length <= 5 * 10^4
  • rectangles[i].length == points[j].length == 2
  • 1 <= li, xj <= 10^9
  • 1 <= hi, yj <= 100
  • 所有 rectangles 互不相同 。
  • 所有 points 互不相同 。

# 解题思路

打比赛的时候一直在搞怎么排序好，但排完后也没想好接着怎么做

注意数据范围，宽的范围是10^9，而高的范围是100。

按高存储不同矩形，当高相同时，将宽按从小到大排序

遍历点时，统计高度在[1,100]范围内，用二分计算每个高度合法的矩形数量

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

const int MAXN = 101;
class Solution {
public:
    vector<vector<int>> tab;
    vector<int> countRectangles(vector<vector<int>>& rectangles, vector<vector<int>>& points) {
        tab.resize(101);
        for(auto &x:rectangles){
            tab[x[1]].push_back(x[0]);
        }
        for(auto &x:tab){
            sort(x.begin(),x.end());
        }
        vector<int> res;
        for(auto &point:points){
            int x = point[0], y = point[1], cnt = 0;
            for(int height=100;height>=1;height--){
                if(height<y) break;//高度不够
                if(tab[height].empty()) continue;//没有该高度的矩形
                int idx = lower_bound(tab[height].begin(),tab[height].end(),x)-tab[height].begin();//第一个宽度大于等于该宽度的举行索引
                cnt += tab[height].size()-idx;
            }
            res.push_back(cnt);
        }
        return res;
    }
};

# 【差分、线段树等】花期内花的数目

# 题目

给你一个下标从 0 开始的二维整数数组 flowers ，其中 flowers[i] = [starti, endi] 表示第 i 朵花的 花期 从 starti 到 endi （都 包含）。同时给你一个下标从 0 开始大小为 n 的整数数组 persons ，persons[i] 是第 i 个人来看花的时间。

请你返回一个大小为 n 的整数数组 answer ，其中 answer[i]是第 i 个人到达时在花期内花的 数目 。

示例 1：

img

1
2
3
4

输入：flowers = [[1,6],[3,7],[9,12],[4,13]], persons = [2,3,7,11]
输出：[1,2,2,2]
解释：上图展示了每朵花的花期时间，和每个人的到达时间。
对每个人，我们返回他们到达时在花期内花的数目。

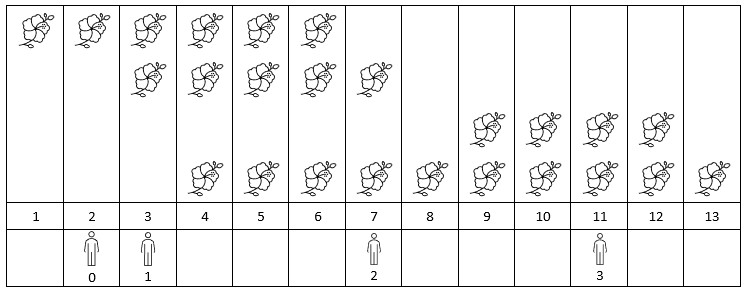
示例 2：

img

1
2
3
4

输入：flowers = [[1,10],[3,3]], persons = [3,3,2]
输出：[2,2,1]
解释：上图展示了每朵花的花期时间，和每个人的到达时间。
对每个人，我们返回他们到达时在花期内花的数目。

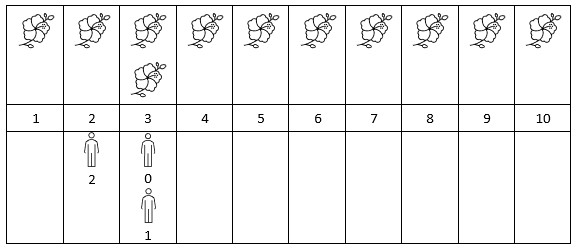
提示：

  • 1 <= flowers.length <= 5 * 10^4
  • flowers[i].length == 2
  • 1 <= starti <= endi <= 10^9
  • 1 <= persons.length <= 5 * 10^4
  • 1 <= persons[i] <= 10^9

# 排序+二分

正在开的花的个数 为所有在此时间节点及之前开放的花的个数减去在时间节点之前凋谢的花的个数

先分别存下花期的开始时间和结束时间，排序

然后二分查找满足条件的花

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {
        vector<int> s,t;
        for(auto &x: flowers){
            s.push_back(x[0]);
            t.push_back(x[1]);
        }
        sort(s.begin(),s.end());
        sort(t.begin(),t.end());

        vector<int> res;
        for(auto &time: persons){
            int all = upper_bound(s.begin(),s.end(),time)-s.begin();//开花期第一个大于当前时间time的花的索引，即有all个开花期小于等于当前时间，也就是最多观赏到all朵花
            int minus = upper_bound(t.begin(),t.end(),time-1)-t.begin();//凋谢时间第一个大于当前时间time-1的花的索引，即有minus个凋谢时间小于等于当前时间-1，也就是说minus个看不到，而这minus个一定在前面all个当中
            // cout<<all<<' '<<minus<<endl;
            res.push_back(all-minus);
        }
        return res;
    }
};

# 差分

把flowers[i]分成两个点：(flowers[i][0],-INF)表示花期的开始，(flowers[i][1],INF)表示花期的结束，每个询问看成一个点(person[i],i)

这样做是为了方便排序。维护变量now，表示花的变化量，遇到花期开始则now++，遇到花期结束则now–，询问答案就是当前now值

代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    typedef pair<int, int> pii;
    const int INF = 1e9;

public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {
        vector<pii> vec;
        for (auto &f : flowers) vec.push_back(pii(f[0], -INF)), vec.push_back(pii(f[1], INF));
        for (int i = 0; i < persons.size(); i++) vec.push_back(pii(persons[i], i));
        sort(vec.begin(), vec.end());

        vector<int> ans(persons.size());
        int now = 0;
        for (pii p : vec) {
            if (p.second == -INF) now++;
            else if (p.second == INF) now--;
            else ans[p.second] = now;
        }
        return ans;
    }
};

# 动态开点线段树

记录在力扣题解上：

动态开点线段树（C++）【区间修改+单点查询】

代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

#define ll long long
const int MAXM = 4e6+5;
const int MAXN = 1e9+5;
struct{
    int lson,rson;
    ll sum,tag;
}T[MAXM];
int tot,root;
class Solution {
public:
    void push_up(int &p){
        T[p].sum = T[T[p].lson].sum + T[T[p].rson].sum;
    }
    void push_down(int &p, int l, int r){
        if(!T[p].tag) return;
        if(!T[p].lson){
            T[p].lson = ++tot;
            T[T[p].lson] = {0,0,0,0};
        }
        if(!T[p].rson){
            T[p].rson = ++tot;
            T[T[p].rson] = {0,0,0,0};
        }
        int mid = (l+r)>>1;
        T[T[p].lson].tag += T[p].tag;
        T[T[p].rson].tag += T[p].tag;
        T[T[p].lson].sum += (mid-l+1)*T[p].tag;
        T[T[p].rson].sum += (r-mid)*T[p].tag;
        T[p].tag = 0;
    }
    void update(int &p, int l, int r, int nl, int nr, int k){
        if(!p){
            p = ++tot;
            T[p] = {0,0,0,0};
        }
        if(nl<=l && nr>=r){
            T[p].sum += k*(T[p].rson-T[p].lson+1);
            T[p].tag += k;
            return;
        }
        push_down(p,l,r);
        int mid = (l+r)>>1;
        if(nl<=mid) update(T[p].lson,l,mid,nl,nr,k);
        if(nr>mid) update(T[p].rson,mid+1,r,nl,nr,k);
        push_up(p);
    }
    int query(int p,int l, int r, int nl, int nr){
        if(nl<=l && nr>=r) return T[p].sum;
        int res = 0, mid = (l+r)>>1;
        push_down(p,l,r);
        if(nl<=mid) res+=query(T[p].lson,l,mid,nl,nr);
        if(nr>mid) res+=query(T[p].rson,mid+1,r,nl,nr);
        return res;
    }
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {
        tot = 0;
        root = 0;
        for(auto &x:flowers){
            update(root,1,MAXN,x[0],x[1],1);
        }
        vector<int> res;
        for(auto &x:persons){
            res.push_back(query(root,1,MAXN,x,x));
        }
        return res;
    }
};

# 离散化+线段树

还可以利用离散化+线段树，它们的目的都是尽量减少所需要的节点数目。

虽然时间值域很大，达$10^9$，但是注意到花期+每个人的到达时间 总共的时间数量不超过 $2\times 5e4 + 5e4$，所以可以进行离散化，*将所有时间放在一起排序后，用它们在数组中的索引来代替原来的值即可*。

然后可以进行去重，除掉重复的元素。

有个细节是实现的线段树节点编号是以1开始索引的，所以后面使用区间范围时要+1（不然是0开始）

代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
const int MAXN = 150000+5;//2*5e4+5e4
vector<int> times;
struct{
    long long sum,tag;
}T[MAXN<<2];
void push_up(int p){
    T[p].sum = T[ls(p)].sum+T[rs(p)].sum;
}
void push_down(int p, int l, int r){
    if(!T[p].tag) return;
    T[ls(p)].tag += T[p].tag;
    T[rs(p)].tag += T[p].tag;
    int mid = (l+r)>>1;
    T[ls(p)].sum += T[p].tag*(mid-l+1);
    T[rs(p)].sum += T[p].tag*(r-mid);
    T[p].tag = 0;
}
void build(int p, int l, int r){
    if(l==r){
        T[p].sum=0;
        T[p].tag=0;
        return;
    }
    T[p].sum=0,T[p].tag=0;
    int mid = (l+r)>>1;
    build(ls(p),l,mid);
    build(rs(p),mid+1,r);
    push_up(p);
}
void update(int p, int l, int r, int nl, int nr, int k){
    if(nl<=l && nr>=r){
        T[p].tag += k;
        T[p].sum += (r-l+1)*k;
        return;
    }
    push_down(p,l,r);
    int mid = (l+r)>>1;
    if(nl<=mid) update(ls(p),l,mid,nl,nr,k);
    if(nr>mid) update(rs(p),mid+1,r,nl,nr,k);
    push_up(p);
}
int query(int p, int l, int r, int nl, int nr){
    if(nl<=l && nr>=r) return T[p].sum;
    push_down(p,l,r);
    int res = 0, mid = (l+r)>>1;
    if(nl<=mid) res += query(ls(p),l,mid,nl,nr);
    if(nr>mid) res += query(rs(p),mid+1,r,nl,nr);
    return res;
}
class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {
        int n = flowers.size()*2+persons.size();
        times.resize(n);
        for(int i=0;i<flowers.size();i++){
            times[i<<1] = flowers[i][0];
            times[i<<1|1] = flowers[i][1];
        }
        for(int i=0;i<persons.size();i++){
            times[(flowers.size()<<1)+i] = persons[i];
        }
        sort(times.begin(),times.end());
        times.erase(unique(times.begin(),times.end()),times.end());
        n = times.size();
        //离散化后排序去重，后面在用它们的值时利用它们在times数组中的索引即可
        build(1,1,n);
        for(auto &x: flowers){
            int nl = lower_bound(times.begin(),times.end(),x[0])-times.begin()+1;
            int nr = lower_bound(times.begin(),times.end(),x[1])-times.begin()+1;
            update(1,1,n,nl,nr,1);
        }
        vector<int> res;
        for(auto &x:persons){
            int idx = lower_bound(times.begin(),times.end(),x)-times.begin()+1;
            res.push_back(query(1,1,n,idx,idx));
        }
        return res;

    }
};
线段树
Licensed under CC BY-NC-SA 4.0
Last updated on Apr 25, 2022 00:00 UTC
© 2020 - 2024 おう てつ の blog
Built with Hugo
Theme Stack designed by Jimmy