
【模拟】字符串中最大的3位相同数字
题目
给你一个字符串 num ,表示一个大整数。如果一个整数满足下述所有条件,则认为该整数是一个 优质整数 :
- 该整数是
num 的一个长度为 3 的 子字符串 。 - 该整数由唯一一个数字重复
3 次组成。
以字符串形式返回 最大的优质整数 。如果不存在满足要求的整数,则返回一个空字符串 "" 。
注意:
- 子字符串 是字符串中的一个连续字符序列。
num 或优质整数中可能存在 前导零 。
示例 1:
1
2
3
4
| 输入:num = "6777133339"
输出:"777"
解释:num 中存在两个优质整数:"777" 和 "333" 。
"777" 是最大的那个,所以返回 "777" 。
|
示例 2:
1
2
3
| 输入:num = "2300019"
输出:"000"
解释:"000" 是唯一一个优质整数。
|
示例 3:
1
2
3
| 输入:num = "42352338"
输出:""
解释:不存在长度为 3 且仅由一个唯一数字组成的整数。因此,不存在优质整数。
|
提示:
3 <= num.length <= 1000num 仅由数字(0 - 9)组成
解题思路
按题意模拟即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
string largestGoodInteger(string num) {
set<string> st;
int n = num.size();
for(int i=0;i<n-2;i++){
if(num[i]==num[i+1] && num[i+1]==num[i+2]){
st.insert(num.substr(i,3));
}
}
if(st.empty()) return "";
else return *st.rbegin();
}
};
|
偷学代码
1
2
3
4
5
6
7
8
9
10
11
12
| class Solution {
public:
string largestGoodInteger(string s) {
string ans;
for(int i = 2; i < s.size(); ++i) {
if(s[i] == s[i-1] && s[i-1] == s[i-2]) {
ans = max(ans, string(3, s[i]));
}
}
return ans;
}
};
|
【DFS】统计值等于子树平均值的节点数
题目
给你一棵二叉树的根节点 root ,找出并返回满足要求的节点数,要求节点的值等于其 子树 中值的 平均值 。
注意:
n 个元素的平均值可以由 n 个元素 求和 然后再除以 n ,并 向下舍入 到最近的整数。root 的 子树 由 root 和它的所有后代组成。
示例 1:
1
2
3
4
5
6
7
8
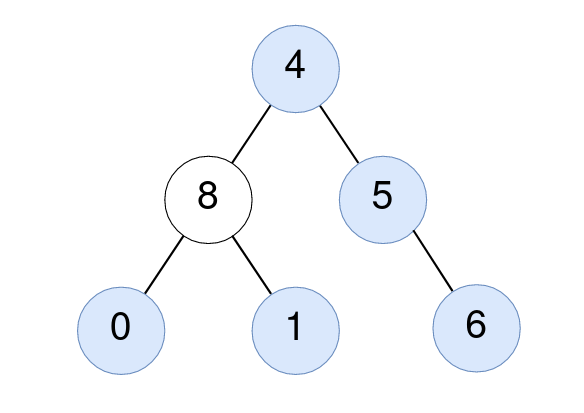
| 输入:root = [4,8,5,0,1,null,6]
输出:5
解释:
对值为 4 的节点:子树的平均值 (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4 。
对值为 5 的节点:子树的平均值 (5 + 6) / 2 = 11 / 2 = 5 。
对值为 0 的节点:子树的平均值 0 / 1 = 0 。
对值为 1 的节点:子树的平均值 1 / 1 = 1 。
对值为 6 的节点:子树的平均值 6 / 1 = 6 。
|
示例 2:

1
2
3
| 输入:root = [1]
输出:1
解释:对值为 1 的节点:子树的平均值 1 / 1 = 1。
|
提示:
- 树中节点数目在范围
[1, 1000] 内 0 <= Node.val <= 1000
解题思路
DFS遍历,返回节点值的总和以及节点个数
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
const int MAXN = 1005;
int res = 0;
pair<int,int> dfs(TreeNode* root){//first:sum second:cnt
if(!root) return {0,0};
auto ls = dfs(root->left);
auto rs = dfs(root->right);
int sum = root->val+ls.first+rs.first;
int cnt = 1 + ls.second+rs.second;
if(sum/cnt==root->val) res++;
return make_pair(sum,cnt);
}
int averageOfSubtree(TreeNode* root) {
dfs(root);
return res;
}
};
|
【DP+乘法原理】统计打字方案数
题目
Alice 在给 Bob 用手机打字。数字到字母的 对应 如下图所示。

为了 打出 一个字母,Alice 需要 按 对应字母 i 次,i 是该字母在这个按键上所处的位置。
- 比方说,为了按出字母
's' ,Alice 需要按 '7' 四次。类似的, Alice 需要按 '5' 两次得到字母 'k' 。 - 注意,数字
'0' 和 '1' 不映射到任何字母,所以 Alice 不 使用它们。
但是,由于传输的错误,Bob 没有收到 Alice 打字的字母信息,反而收到了 按键的字符串信息 。
- 比方说,Alice 发出的信息为
"bob" ,Bob 将收到字符串 "2266622" 。
给你一个字符串 pressedKeys ,表示 Bob 收到的字符串,请你返回 Alice 总共可能发出多少种文字信息 。
由于答案可能很大,将它对 10^9 + 7 取余 后返回。
示例 1:
1
2
3
4
5
6
| 输入:pressedKeys = "22233"
输出:8
解释:
Alice 可能发出的文字信息包括:
"aaadd", "abdd", "badd", "cdd", "aaae", "abe", "bae" 和 "ce" 。
由于总共有 8 种可能的信息,所以我们返回 8 。
|
示例 2:
1
2
3
4
5
| 输入:pressedKeys = "222222222222222222222222222222222222"
输出:82876089
解释:
总共有 2082876103 种 Alice 可能发出的文字信息。
由于我们需要将答案对 109 + 7 取余,所以我们返回 2082876103 % (109 + 7) = 82876089 。
|
提示:
1 <= pressedKeys.length <= 10^5pressedKeys 只包含数字 '2' 到 '9' 。
解题思路
比赛的时候想到是动态规划,往整数拆分那边想,没有第一时间找到递推公式
于是枚举前几项找规律,真发现了不得了的规律,对于2、3、4、5、6、8来说,令dp[i]表示长度为i的按键信息对应的不同文字信息的种数,有dp[i]=dp[i-1]+dp[i-2]+dp[i-3]。对于7、9来说类似。
更正式地:
思路和爬楼梯类似
对于3字母数字来说,令dp[i]表示长度为i的按键信息对应的不同文字信息的种数,初始化dp[1]=1,dp[2]=2,dp[3]=4。考虑dp[i],可以将末尾的1个、2个或3个字符单独视作一个字母,得出状态转移方程
1
| dp[i] = dp[i-1]+dp[i-2]+dp[i-3];
|
4字母数字类似。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution {
public:
const int MAXN = 1e5+3;
const int MOD = 1e9+7;
vector<long long> dp;
vector<long long> dp2;
int countTexts(string pressedKeys) {
int n = pressedKeys.size();
dp.assign(MAXN,0);
dp[1]=1,dp[2]=2,dp[3]=4;
for(int i=4;i<=n;i++) dp[i] = (dp[i-1]+dp[i-2]+dp[i-3])%MOD;
dp2.assign(MAXN,0);
dp2[1]=1,dp2[2]=2,dp2[3]=4,dp2[4]=8;
for(int i=5;i<=n;i++) dp2[i] = (dp2[i-1]+dp2[i-2]+dp2[i-3]+dp2[i-4])%MOD;
long long res = 1;
unordered_map<string,int> tab;
int start=0;
for(int i=0;i<n-1;i++){//如果最后一个字符是单独的一个字符,会被忽略掉,但不会影响结果
if(pressedKeys[i]==pressedKeys[i+1]){
if(i==n-2){
string str = pressedKeys.substr(start,i+1-start+1);
tab[str]++;
}
}else{
string str = pressedKeys.substr(start,i-start+1);
tab[str]++;
start=i+1;
}
}
for(auto &x: tab){
string s = x.first;
int cnt = x.second;
if(s[0]=='7'||s[0]=='9') {
for(int i=1;i<=cnt;i++)
res = (res*dp2[s.size()])%MOD;
}else{
for(int i=1;i<=cnt;i++)
res = (res*dp[s.size()])%MOD;
}
}
return res;
}
};
|
偷学代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| int MOD = 1e9 + 7;
class Solution {
public:
int countTexts(string a) {
vector <int> dp0, dp1;
dp0.resize(a.size() + 5);
dp1.resize(a.size() + 5);
dp0[0] = dp1[0] = 1;
for (int i = 1; i < dp0.size(); i++) {
for (int j = 1; j <= 3 && j <= i; j++) {
dp0[i] = (dp0[i] + dp0[i - j]) % MOD;
}
for (int j = 1; j <= 4 && j <= i; j++) {
dp1[i] = (dp1[i] + dp1[i - j]) % MOD;
}
}
int ans = 1;
for (int i = 0; i < a.size(); i++) {
int j = i;
while (j + 1 < a.size() && a[j + 1] == a[i]) {
j++;
}
int len = j - i + 1;
i = j;
if (a[i] == '7' || a[i] == '9') {
ans = (long long)ans * dp1[len] % MOD;
} else {
ans = (long long)ans * dp0[len] % MOD;
}
}
return ans;
}
};
|
【DP/DFS+有效括号】检查是否有合法括号字符串路径
题目
一个括号字符串是一个 非空 且只包含 '(' 和 ')' 的字符串。如果下面 任意 条件为 真 ,那么这个括号字符串就是 合法的 。
- 字符串是
() 。 - 字符串可以表示为
AB(A 连接 B),A 和 B 都是合法括号序列。 - 字符串可以表示为
(A) ,其中 A 是合法括号序列。
给你一个 m x n 的括号网格图矩阵 grid 。网格图中一个 合法括号路径 是满足以下所有条件的一条路径:
- 路径开始于左上角格子
(0, 0) 。 - 路径结束于右下角格子
(m - 1, n - 1) 。 - 路径每次只会向 下 或者向 右 移动。
- 路径经过的格子组成的括号字符串是 合法 的。
如果网格图中存在一条 合法括号路径 ,请返回 true ,否则返回 false 。
示例 1:

1
2
3
4
5
6
| 输入:grid = [["(","(","("],[")","(",")"],["(","(",")"],["(","(",")"]]
输出:true
解释:上图展示了两条路径,它们都是合法括号字符串路径。
第一条路径得到的合法字符串是 "()(())" 。
第二条路径得到的合法字符串是 "((()))" 。
注意可能有其他的合法括号字符串路径。
|
示例 2:

1
2
3
| 输入:grid = [[")",")"],["(","("]]
输出:false
解释:两条可行路径分别得到 "))(" 和 ")((" 。由于它们都不是合法括号字符串,我们返回 false 。
|
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 100grid[i][j] 要么是 '(' ,要么是 ')' 。
解题思路
写第3题花了太多时间了,这题就没写。
补题时补了一些括号匹配的题。
前置知识:判断一个括号序列是否合法,只需要判断每个位置上左括号总数量大于等于右括号总数量,并且最后左括号数量和右括号数量相等。
DFS
如果知道如何判断括号序列是否合法的话,DFS框架还是很容易想的
离谱的是,两种差不多的写法,一种超时,一种过了
两者的区别是,过了的代码中,将now<0判错的语句提到了前面。
下面这种过了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public:
int n,m;
vector<vector<char>> G;
int dp[101][101][202];
bool dfs(int x, int y, int now){
if(x>=n||y>=m) return false;
if(now>n-x+m-y-1 || now<0) return false;
if(dp[x][y][now]) return false;
if(x==n-1 && y==m-1){
return now==1;
}
dp[x][y][now]=1;
if(G[x][y]=='(') now++;
else now--;
return dfs(x+1,y,now)||dfs(x,y+1,now);
}
bool hasValidPath(vector<vector<char>>& grid) {
n = grid.size(), m = grid[0].size();
G = grid;
if(grid[0][0]==')'||grid[n-1][m-1]=='('||(m+n-1)&1) return false;
memset(dp,0,sizeof(dp));
return dfs(0,0,0);
}
};
|
这种超时了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
int n,m;
vector<vector<char>> G;
int dp[101][101][202];
bool dfs(int x, int y, int now){
if(x>=n||y>=m) return false;
if(now>n-x+m-y-1) return false;
if(dp[x][y][now]) return false;
if(x==n-1 && y==m-1){
now--;
if(now==0) return true;
else return false;
}
if(G[x][y]=='(') now++;
else now--;
if(now<0) {
return false;
}
dp[x][y][now]=1;
return dfs(x+1,y,now)||dfs(x,y+1,now);
}
bool hasValidPath(vector<vector<char>>& grid) {
n = grid.size(), m = grid[0].size();
G = grid;
if(grid[0][0]==')'||grid[n-1][m-1]=='('||(m+n-1)&1) return false;
memset(dp,0,sizeof(dp));
return dfs(0,0,0);
}
};
|
DP
令dp[i,j,k]表示grid[i,j]且左括号净计数为k的状态是否存在
最后判断dp[n-1][m-1][0]是否为真即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public:
bool hasValidPath(vector<vector<char>>& grid) {
int n = grid.size(),m = grid[0].size();
if((n+m-1)&1||grid[0][0]==')'||grid[n-1][m-1]=='(') return false;
int maxlen=m+n-1;
bool dp[n][m][maxlen+1];
memset(dp,0,sizeof(dp));
//dp[i][j][k] grid[i][j]左括号净计数为k的状态是否存在
dp[0][0][1] = true;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(i==0&&j==0) continue;
int c=grid[i][j]=='('?1:-1;
for(int k=0;k<=maxlen;k++){
if(k-c<0||k-c>maxlen) continue;
if(i-1>=0)//上到下
dp[i][j][k] = dp[i][j][k]||dp[i-1][j][k-c];
if(j-1>=0)//左到右
dp[i][j][k] = dp[i][j][k]||dp[i][j-1][k-c];
}
}
}
return dp[n-1][m-1][0];
}
};
|






