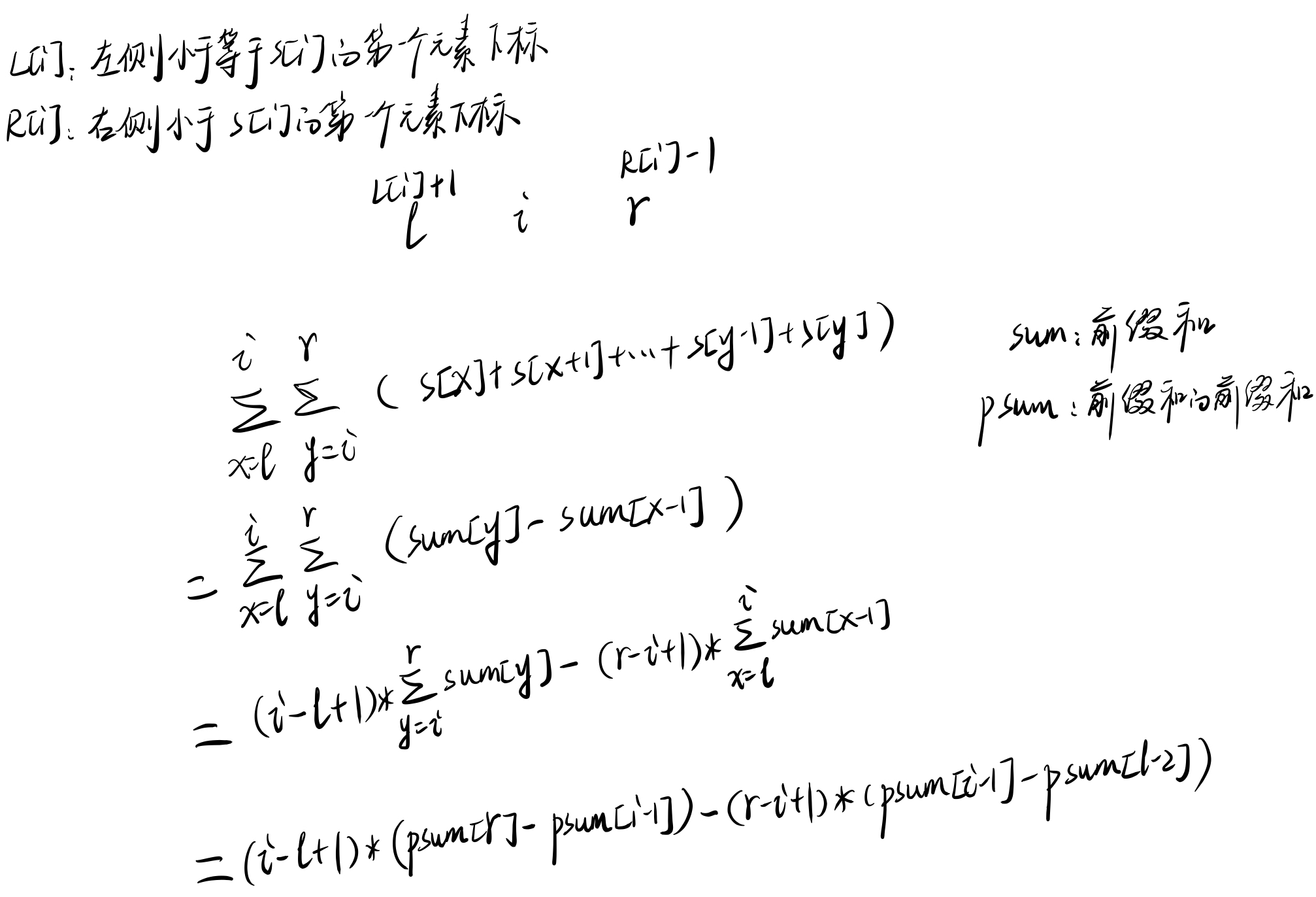Featured image of post LeetCode第294场周赛总结
leetcode contest

LeetCode第294场周赛总结

1350/6640

image-20220523111757716

# 【模拟】字母在字符串中的百分比

# 题目

给你一个字符串 s 和一个字符 letter ，返回在 s 中等于 letter 字符所占的 百分比 ，向下取整到最接近的百分比。

示例 1：

1
2
3
4

输入：s = "foobar", letter = "o"
输出：33
解释：
等于字母 'o' 的字符在 s 中占到的百分比是 2 / 6 * 100% = 33% ，向下取整，所以返回 33 。

示例 2：

1
2
3
4

输入：s = "jjjj", letter = "k"
输出：0
解释：
等于字母 'k' 的字符在 s 中占到的百分比是 0% ，所以返回 0 。

提示：

  • 1 <= s.length <= 100
  • s 由小写英文字母组成
  • letter 是一个小写英文字母

# 解题思路

按题意模拟即可。

# 代码

1
2
3
4
5
6
7
8
9

class Solution {
public:
    int percentageLetter(string s, char letter) {
        int n = s.size();
        int cnt=0;
        for(auto &x: s) if(x==letter) cnt++;
        return (cnt*100/n);
    }
};

# 【贪心】装满石头的背包的最大数量

# 题目

现有编号从 0 到 n - 1 的 n 个背包。给你两个下标从 0 开始的整数数组 capacity 和 rocks 。第 i 个背包最大可以装 capacity[i] 块石头，当前已经装了 rocks[i] 块石头。另给你一个整数 additionalRocks ，表示你可以放置的额外石头数量，石头可以往 任意 背包中放置。

请你将额外的石头放入一些背包中，并返回放置后装满石头的背包的 最大 数量*。*

示例 1：

1
2
3
4
5
6
7
8
9

输入：capacity = [2,3,4,5], rocks = [1,2,4,4], additionalRocks = 2
输出：3
解释：
1 块石头放入背包 0 ，1 块石头放入背包 1 。
每个背包中的石头总数是 [2,3,4,4] 。
背包 0 、背包 1 和 背包 2 都装满石头。
总计 3 个背包装满石头，所以返回 3 。
可以证明不存在超过 3 个背包装满石头的情况。
注意，可能存在其他放置石头的方案同样能够得到 3 这个结果。

示例 2：

1
2
3
4
5
6
7
8
9

输入：capacity = [10,2,2], rocks = [2,2,0], additionalRocks = 100
输出：3
解释：
8 块石头放入背包 0 ，2 块石头放入背包 2 。
每个背包中的石头总数是 [10,2,2] 。
背包 0 、背包 1 和背包 2 都装满石头。
总计 3 个背包装满石头，所以返回 3 。
可以证明不存在超过 3 个背包装满石头的情况。
注意，不必用完所有的额外石头。

提示：

  • n == capacity.length == rocks.length
  • 1 <= n <= 5 * 10^4
  • 1 <= capacity[i] <= 10^9
  • 0 <= rocks[i] <= capacity[i]
  • 1 <= additionalRocks <= 10^9

# 解题思路

将剩余容量排序，从小往大填

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    int maximumBags(vector<int>& capacity, vector<int>& rocks, int additionalRocks) {
        int n = capacity.size();
        vector<int> a;
        for(int i=0;i<n;i++){
            a.push_back(capacity[i]-rocks[i]);
        }
        sort(a.begin(),a.end());
        int res = 0;
        for(auto &x: a){
            if(x==0) res++;
            else{
                additionalRocks -= x;
                if(additionalRocks>=0) res++;
                else break;
            }
        }
        return res;
    }
};

# 【枚举】表示一个折线图的最少线段数

# 题目

给你一个二维整数数组 stockPrices ，其中 stockPrices[i] = [dayi, pricei] 表示股票在 dayi 的价格为 pricei 。折线图 是一个二维平面上的若干个点组成的图，横坐标表示日期，纵坐标表示价格，折线图由相邻的点连接而成。比方说下图是一个例子：

请你返回要表示一个折线图所需要的 最少线段数 。

示例 1：

1
2
3
4
5
6
7
8
9

输入：stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]
输出：3
解释：
上图为输入对应的图，横坐标表示日期，纵坐标表示价格。
以下 3 个线段可以表示折线图：
- 线段 1 （红色）从 (1,7) 到 (4,4) ，经过 (1,7) ，(2,6) ，(3,5) 和 (4,4) 。
- 线段 2 （蓝色）从 (4,4) 到 (5,4) 。
- 线段 3 （绿色）从 (5,4) 到 (8,1) ，经过 (5,4) ，(6,3) ，(7,2) 和 (8,1) 。
可以证明，无法用少于 3 条线段表示这个折线图。

示例 2：

1
2
3
4

输入：stockPrices = [[3,4],[1,2],[7,8],[2,3]]
输出：1
解释：
如上图所示，折线图可以用一条线段表示。

提示：

  • 1 <= stockPrices.length <= 105
  • stockPrices[i].length == 2
  • 1 <= dayi, pricei <= 109
  • 所有 dayi 互不相同 。

# 解题思路

这题真的醉了，一开始用斜率判断是否三点贡献，最后有两个测试用例过不了，WA了两发才知道是精度问题

以后涉及到除法的，小心精度问题

枚举一遍就行了，我写成了动规的形式

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
public:
    bool isok(vector<int> &a, vector<int> &b, vector<int> &c){//是否三点共线
        if(c[1]==b[1] && b[1]==a[1]) return true;
        // if(1.00*(c[1]-b[1])/(1.00*(c[0]-b[0]))==1.00*(b[1]-a[1])/(1.00*(b[0]-a[0]))) return true;
        // else return false;
        long long x = 1ll*(c[0]-b[0])*(b[1]-a[1]);
        long long y = 1ll*(c[1]-b[1])*(b[0]-a[0]);
        return x==y;
    }
    int minimumLines(vector<vector<int>>& stockPrices) {
        int n = stockPrices.size();
        if(n==1) return 0;
        if(n==2) return 1;
        sort(stockPrices.begin(), stockPrices.end());
        // cout<<isok(stockPrices[2],stockPrices[3],stockPrices[4]);
        vector<int> dp(n,0);
        dp[0] = 0;
        dp[1] = 1;
        for(int i=2;i<n;i++){
            if(isok(stockPrices[i-2],stockPrices[i-1],stockPrices[i])) dp[i] = dp[i-1];
            else dp[i] = dp[i-1]+1;
        }
     
        return dp[n-1];
    }
};

# 【计算贡献+单调栈+前缀和】巫师的总力量和

# 题目

作为国王的统治者，你有一支巫师军队听你指挥。

给你一个下标从 0 开始的整数数组 strength ，其中 strength[i] 表示第 i 位巫师的力量值。对于连续的一组巫师（也就是这些巫师的力量值是 strength 的 子数组），总力量 定义为以下两个值的 乘积 ：

巫师中 最弱 的能力值。

组中所有巫师的个人力量值 之和 。

请你返回 所有 巫师组的 总 力量之和。由于答案可能很大，请将答案对 10^9 + 7 取余 后返回。

子数组 是一个数组里 非空 连续子序列。

示例 1：

输入：strength = [1,3,1,2] 输出：44 解释：以下是所有连续巫师组：

  • [1,3,1,2] 中 [1] ，总力量值为 min([1]) * sum([1]) = 1 * 1 = 1
  • [1,3,1,2] 中 [3] ，总力量值为 min([3]) * sum([3]) = 3 * 3 = 9
  • [1,3,1,2] 中 [1] ，总力量值为 min([1]) * sum([1]) = 1 * 1 = 1
  • [1,3,1,2] 中 [2] ，总力量值为 min([2]) * sum([2]) = 2 * 2 = 4
  • [1,3,1,2] 中 [1,3] ，总力量值为 min([1,3]) * sum([1,3]) = 1 * 4 = 4
  • [1,3,1,2] 中 [3,1] ，总力量值为 min([3,1]) * sum([3,1]) = 1 * 4 = 4
  • [1,3,1,2] 中 [1,2] ，总力量值为 min([1,2]) * sum([1,2]) = 1 * 3 = 3
  • [1,3,1,2] 中 [1,3,1] ，总力量值为 min([1,3,1]) * sum([1,3,1]) = 1 * 5 = 5
  • [1,3,1,2] 中 [3,1,2] ，总力量值为 min([3,1,2]) * sum([3,1,2]) = 1 * 6 = 6
  • [1,3,1,2] 中 [1,3,1,2] ，总力量值为 min([1,3,1,2]) * sum([1,3,1,2]) = 1 * 7 = 7 所有力量值之和为 1 + 9 + 1 + 4 + 4 + 4 + 3 + 5 + 6 + 7 = 44 。 示例 2：

输入：strength = [5,4,6] 输出：213 解释：以下是所有连续巫师组：

  • [5,4,6] 中 [5] ，总力量值为 min([5]) * sum([5]) = 5 * 5 = 25
  • [5,4,6] 中 [4] ，总力量值为 min([4]) * sum([4]) = 4 * 4 = 16
  • [5,4,6] 中 [6] ，总力量值为 min([6]) * sum([6]) = 6 * 6 = 36
  • [5,4,6] 中 [5,4] ，总力量值为 min([5,4]) * sum([5,4]) = 4 * 9 = 36
  • [5,4,6] 中 [4,6] ，总力量值为 min([4,6]) * sum([4,6]) = 4 * 10 = 40
  • [5,4,6] 中 [5,4,6] ，总力量值为 min([5,4,6]) * sum([5,4,6]) = 4 * 15 = 60 所有力量值之和为 25 + 16 + 36 + 36 + 40 + 60 = 213 。

提示：

1 <= strength.length <= 10^5

1 <= strength[i] <= 10^9

来源：力扣（LeetCode） 链接：https://leetcode.cn/problems/sum-of-total-strength-of-wizards 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

# 解题思路

一眼计算贡献，但之前做的都是按照动态规划的思路做的，比赛后发现这题推不了递推式，还是得采用计算单个元素的贡献范围以及贡献值。

对于每个元素s[i]，找到其贡献范围[l, r]，为了避免相同元素重复计算贡献，注意L[i]和R[i]的含义

注意取模，出现减法的话要加个MOD再模

计算贡献的时候，这个表达式要敢于计算

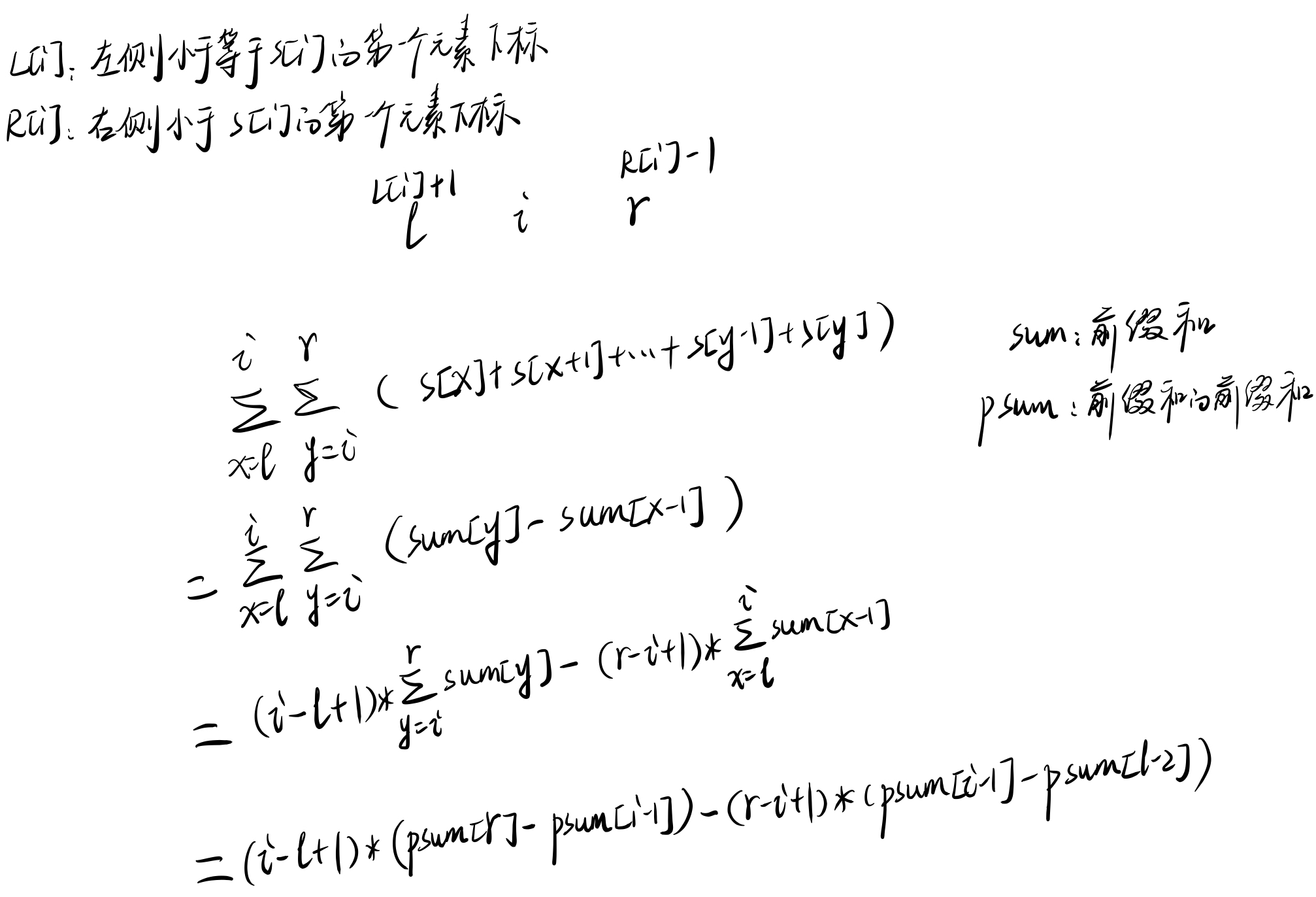
image-20220523114004671

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

const int MOD = 1e9+7;
class Solution {
public:
    int totalStrength(vector<int>& strength) {
        int n = strength.size();
        if(n==1) return (1ll*strength[0]*strength[0])%MOD;
        vector<int> L(n,0);//L[i] 左侧小于等于s[i]的第一个位置
        stack<int> stk;
        L[0]=-1;
        stk.push(0);
        for(int i=1;i<n;i++){
            while(!stk.empty() && strength[i]<strength[stk.top()]) stk.pop();
            if(stk.empty()) L[i]=-1;
            else L[i]=stk.top();
            stk.push(i);
        }
       
        vector<int> R(n,n);//R[i] 右侧小于s[i]的第一个位置
        R[n-1]=n;
        while(!stk.empty()) stk.pop();
        stk.push(n-1);
        for(int i=n-2;i>=0;i--){
            while(!stk.empty() && strength[i]<=strength[stk.top()]) stk.pop();
            if(stk.empty()) R[i]=n;
            else R[i]=stk.top();
            stk.push(i);
        }
       
        vector<long long> sum(n+1,0), psum(n+1,0);
        sum[0]=0;//前缀和
        psum[0]=0;//前缀和的前缀和
        for(int i=1;i<=n;i++){//注意和思路中表达式中 有偏移
            sum[i] = (sum[i-1]+strength[i-1])%MOD;
            psum[i] = (psum[i-1]+sum[i])%MOD;
        }
        function<long long(int)> p = [&](int idx){
            if(idx<=0) return 1ll*0;
            if(idx>=n+1) return psum[n];
            return psum[idx];
        };
        long long res = 0;
        for(int i=0;i<n;i++){
            int l = L[i]+1, r = R[i]-1;
            long long partI = (i-l+1)*(p(r+1)-p(i))%MOD;
            long long partII= (r-i+1)*(p(i)-p(l-1))%MOD;
            res = (res+strength[i]*(partI-partII)+MOD)%MOD;
        }
        
        return res;
    }
};
计算贡献
Licensed under CC BY-NC-SA 4.0
Last updated on May 23, 2022 00:00 UTC
© 2020 - 2024 おう てつ の blog
Built with Hugo
Theme Stack designed by Jimmy