LeetCode第297场周赛总结

【模拟】计算应缴税款总额

题目

给你一个下标从 0 开始的二维整数数组 brackets ，其中 brackets[i] = [upperi, percenti] ，表示第 i 个税级的上限是 upperi ，征收的税率为 percenti 。税级按上限 从低到高排序（在满足 0 < i < brackets.length 的前提下，upperi-1 < upperi）。

税款计算方式如下：

不超过 upper0 的收入按税率 percent0 缴纳
接着 upper1 - upper0 的部分按税率 percent1 缴纳
然后 upper2 - upper1 的部分按税率 percent2 缴纳
以此类推

给你一个整数 income 表示你的总收入。返回你需要缴纳的税款总额。与标准答案误差不超 10-5 的结果将被视作正确答案。

示例 1：

1
2
3
4
5
6
7
输入：brackets = [[3,50],[7,10],[12,25]], income = 10
输出：2.65000
解释：
前 $3 的税率为 50% 。需要支付税款 $3 * 50% = $1.50 。
接下来 $7 - $3 = $4 的税率为 10% 。需要支付税款 $4 * 10% = $0.40 。
最后 $10 - $7 = $3 的税率为 25% 。需要支付税款 $3 * 25% = $0.75 。
需要支付的税款总计 $1.50 + $0.40 + $0.75 = $2.65 。

示例 2：

1
2
3
4
5
6
输入：brackets = [[1,0],[4,25],[5,50]], income = 2
输出：0.25000
解释：
前 $1 的税率为 0% 。需要支付税款 $1 * 0% = $0 。
剩下 $1 的税率为 25% 。需要支付税款 $1 * 25% = $0.25 。
需要支付的税款总计 $0 + $0.25 = $0.25 。

示例 3：

1
2
3
4
输入：brackets = [[2,50]], income = 0
输出：0.00000
解释：
没有收入，无需纳税，需要支付的税款总计 $0 。

提示：

1 <= brackets.length <= 100
1 <= upperi <= 1000
0 <= percenti <= 100
0 <= income <= 1000
upperi 按递增顺序排列
upperi 中的所有值 互不相同
最后一个税级的上限大于等于 income

解题思路

简单模拟。

WA了一发，在income<=b[0][0]时就可以直接返回了，否则的话后面要判断rst是否大于0

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    double calculateTax(vector<vector<int>>& brackets, int income) {
        int n = brackets.size();
        double res = 0.0;
        if(income<=brackets[0][0]) res = 1.00*income*brackets[0][1]/100;
        else res = brackets[0][0]*1.00*brackets[0][1]/100;
        
        for(int i=1;i<n;i++){
            if(income>=brackets[i][0]){
                int rst = brackets[i][0]-brackets[i-1][0];
                res += 1.00*rst*brackets[i][1]/100;
            }else{
                int rst = income-brackets[i-1][0];
                if(rst>0) res += 1.00*rst*brackets[i][1]/100;
                break;
            }
        }
        return res;
    }
};

【动态规划】网格中的最小路径代价

题目

给你一个下标从 0 开始的整数矩阵 grid ，矩阵大小为 m x n ，由从 0 到 m * n - 1 的不同整数组成。你可以在此矩阵中，从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ，且满足 x < m - 1 ，你可以移动到 (x + 1, 0), (x + 1, 1), …, (x + 1, n - 1) 中的任何一个单元格。注意： 在最后一行中的单元格不能触发移动。

每次可能的移动都需要付出对应的代价，代价用一个下标从 0 开始的二维数组 moveCost 表示，该数组大小为 (m * n) x n ，其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。

grid 一条路径的代价是：所有路径经过的单元格的 值之和 加上所有移动的 代价之和 。从 第一行 任意单元格出发，返回到达 最后一行 任意单元格的最小路径代价*。*

示例 1：

1
2
3
4
5
6
7
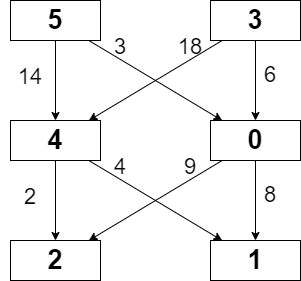
输入：grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
输出：17
解释：最小代价的路径是 5 -> 0 -> 1 。
- 路径途经单元格值之和 5 + 0 + 1 = 6 。
- 从 5 移动到 0 的代价为 3 。
- 从 0 移动到 1 的代价为 8 。
路径总代价为 6 + 3 + 8 = 17 。

示例 2：

1
2
3
4
5
6
7
输入：grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
输出：6
解释：
最小代价的路径是 2 -> 3 。 
- 路径途经单元格值之和 2 + 3 = 5 。 
- 从 2 移动到 3 的代价为 1 。 
路径总代价为 5 + 1 = 6 。

提示：

m == grid.length
n == grid[i].length
2 <= m, n <= 50
grid 由从 0 到 m * n - 1 的不同整数组成
moveCost.length == m * n
moveCost[i].length == n
1 <= moveCost[i][j] <= 100

解题思路

简单路径规划类DP

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
const int INF = 0x3f3f3f3f;
class Solution {
public:
    int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
        int n = grid.size(), m = grid[0].size();
        int res = INF;
        vector<vector<int>> dp(n,vector<int>(m,INF));
        for(int j=0;j<m;j++){
            dp[0][j] = grid[0][j];
        }
        for(int i=1;i<n;i++){
            for(int j=0;j<m;j++){
                for(int k=0;k<m;k++){
                    dp[i][j]=min(dp[i][j], grid[i][j]+dp[i-1][k]+moveCost[grid[i-1][k]][j]);
                }
            }
        }
        for(int j=0;j<m;j++){
            res = min(res,dp[n-1][j]);
        }
        return res;
    }
};

【DFS/状压DP】公平分发饼干

题目

给你一个整数数组 cookies ，其中 cookies[i] 表示在第 i 个零食包中的饼干数量。另给你一个整数 k 表示等待分发零食包的孩子数量，所有零食包都需要分发。在同一个零食包中的所有饼干都必须分发给同一个孩子，不能分开。

分发的 不公平程度 定义为单个孩子在分发过程中能够获得饼干的最大总数。

返回所有分发的最小不公平程度。

示例 1：

1
2
3
4
5
6
7
输入：cookies = [8,15,10,20,8], k = 2
输出：31
解释：一种最优方案是 [8,15,8] 和 [10,20] 。
- 第 1 个孩子分到 [8,15,8] ，总计 8 + 15 + 8 = 31 块饼干。
- 第 2 个孩子分到 [10,20] ，总计 10 + 20 = 30 块饼干。
分发的不公平程度为 max(31,30) = 31 。
可以证明不存在不公平程度小于 31 的分发方案。

示例 2：

1
2
3
4
5
6
7
8
输入：cookies = [6,1,3,2,2,4,1,2], k = 3
输出：7
解释：一种最优方案是 [6,1]、[3,2,2] 和 [4,1,2] 。
- 第 1 个孩子分到 [6,1] ，总计 6 + 1 = 7 块饼干。 
- 第 2 个孩子分到 [3,2,2] ，总计 3 + 2 + 2 = 7 块饼干。
- 第 3 个孩子分到 [4,1,2] ，总计 4 + 1 + 2 = 7 块饼干。
分发的不公平程度为 max(7,7,7) = 7 。
可以证明不存在不公平程度小于 7 的分发方案。

提示：

2 <= cookies.length <= 8
1 <= cookies[i] <= 10^5
2 <= k <= cookies.length

解题思路

看数据规模，n最大值为8，考虑DFS，一遍过了没优化

也想过可以用状压DP，赛时不敢用不熟练的状压DP

代码

DFS 1.0

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
const int INF = 0x3f3f3f3f;
class Solution {
public:
    vector<int> num;
    vector<int> cook;
    int n,res,k;
    void dfs(int x){
        if(x==n){
            int maxv=0;
            for(auto &p: num){
                maxv = max(maxv,p);
            }
            res = min(res,maxv);
            return;
        }
        for(int i=0;i<k;i++){
            num[i] += cook[x];
            dfs(x+1);
            num[i] -= cook[x];
        }
    }
    int distributeCookies(vector<int>& cookies, int k) {
        n = cookies.size();
        cook = cookies;
        res = INF;
        this->k=k;
        num.assign(k,0);
        
        dfs(0);
        return res;
        
    }
};

DFS 2.0

可以考虑记录当前最大值进行剪枝。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
const int INF = 0x3f3f3f3f;
class Solution {
public:
    vector<int> num;
    vector<int> cook;
    int n,res,k;
    void dfs(int x, int curmax){
        if(curmax>=res) return;
        if(x==n){
            int maxv=0;
            for(auto &p: num){
                maxv = max(maxv,p);
            }
            res = min(res,maxv);
            return;
        }
        int tmpmax=curmax;
        for(int i=0;i<k;i++){
            num[i] += cook[x];
            curmax = max(curmax, cook[x]);
            dfs(x+1,curmax);
            num[i] -= cook[x];
            curmax = tmpmax;
        }
    }
    int distributeCookies(vector<int>& cookies, int k) {
        n = cookies.size();
        cook = cookies;
        res = INF;
        this->k=k;
        num.assign(k,0);
        
        dfs(0,0);
        return res;
        
    }
};

状压DP

主要是考虑第i个孩子状态为state时，枚举前i-1个孩子的子状态j（state的子集）），补集为state^j

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int distributeCookies(vector<int>& cookies, int k) {
        int n = cookies.size();
        vector<int> num(1<<n, 0);//num[state] 饼干状态为state时的饼干数量
        for(int state=0;state<(1<<n);state++){
            int cur=0;
            for(int i=0;i<n;i++){
                if((state>>i)&1) cur+=cookies[i];
            }
            num[state] = cur;
        }
        vector<vector<int>> dp(n, vector<int>(1<<n, 0));
        //dp[i][state] 前i个孩子，选择的饼干状态为state时 单个孩子最大饼干数量的最小值
        for(int state=0;state<(1<<n);state++){
            dp[0][state] = num[state];
        }
        for(int i=1;i<k;i++){
            for(int state=0;state<(1<<n);state++){
                dp[i][state] = INT_MAX;
                for(int j=state;j;j=(j-1)&state){//枚举state的子集
                    dp[i][state]=min(dp[i][state], max(dp[i-1][j],num[state^j]));
                }
            }
        }
        return dp[k-1][(1<<n)-1];
    }
};

状压DP 空间优化

类似于01背包，将第二维逆序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int distributeCookies(vector<int>& cookies, int k) {
        int n = cookies.size();
        vector<int> num(1<<n, 0);//num[state] 饼干状态为state时的饼干数量
        for(int state=0;state<(1<<n);state++){
            int cur=0;
            for(int i=0;i<n;i++){
                if((state>>i)&1) cur+=cookies[i];
            }
            num[state] = cur;
        }
        vector<int> dp(1<<n);
        //dp[i][state] 前i个孩子，选择的饼干状态为state时 单个孩子最大饼干数量的最小值
        dp = num;
        for(int i=1;i<k;i++){
            for(int state=(1<<n)-1;state>=0;state--){
                for(int j=state;j;j=(j-1)&state){//枚举state的子集
                    dp[state]=min(dp[state], max(dp[j],num[state^j]));
                }
            }
        }
        return dp[(1<<n)-1];
    }
};

【枚举+计数】公司命名

题目

给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下：

从 ideas 中选择 2 个不同名字，称为 ideaA 和 ideaB 。
交换 ideaA 和 ideaB 的首字母。
如果得到的两个新名字都不在 ideas 中，那么 ideaA ideaB（串联 ideaA 和 ideaB ，中间用一个空格分隔）是一个有效的公司名字。
否则，不是一个有效的名字。

返回不同且有效的公司名字的数目。

示例 1：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
输入：ideas = ["coffee","donuts","time","toffee"]
输出：6
解释：下面列出一些有效的选择方案：
- ("coffee", "donuts")：对应的公司名字是 "doffee conuts" 。
- ("donuts", "coffee")：对应的公司名字是 "conuts doffee" 。
- ("donuts", "time")：对应的公司名字是 "tonuts dime" 。
- ("donuts", "toffee")：对应的公司名字是 "tonuts doffee" 。
- ("time", "donuts")：对应的公司名字是 "dime tonuts" 。
- ("toffee", "donuts")：对应的公司名字是 "doffee tonuts" 。
因此，总共有 6 个不同的公司名字。

下面列出一些无效的选择方案：
- ("coffee", "time")：在原数组中存在交换后形成的名字 "toffee" 。
- ("time", "toffee")：在原数组中存在交换后形成的两个名字。
- ("coffee", "toffee")：在原数组中存在交换后形成的两个名字。

示例 2：

1
2
3
输入：ideas = ["lack","back"]
输出：0
解释：不存在有效的选择方案。因此，返回 0 。

提示：

2 <= ideas.length <= 5 * 10^4
1 <= ideas[i].length <= 10
ideas[i] 由小写英文字母组成
ideas 中的所有字符串 互不相同

解题思路

赛时想到了要按首字母分组

同时记录每个组后缀相同情况

但赛时还是紧张了，只想到了记录是否有相同后缀，没有去记录有相同后缀的个数！可惜

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
public:
    long long distinctNames(vector<string>& ideas) {
        int n = ideas.size();
        vector<unordered_set<string>> tab(26);
        for(auto &str: ideas){
            int type=str[0]-'a';
            string suf(str.begin()+1,str.end());
            tab[type].insert(suf);
        }
        
        long long res = 0;
        int same[26][26];
        memset(same,0,sizeof(same));
        

        for(int i=0;i<26;i++){
            if(tab[i].empty()) continue;
            for(int j=0;j<26;j++){
                if(i==j||tab[j].empty()) continue;
                same[i][j]=0;//以i开头和以j开头的字符串相同后缀的个数
                for(auto &str: tab[i]){
                    if(tab[j].count(str)){
                        same[i][j]++;
                    }
                }
            }
        }
        
        for(int i=0;i<26;i++){
            if(tab[i].empty()) continue;
            for(int j=0;j<26;j++){
                if(i==j||tab[j].empty()) continue;
                // for(auto &str: tab[i]){
                //     if(!tab[j].count(str)){
                //         res += tab[j].size()-same[i][j];
                //     }
                // }
                res+=tab[i].size()*tab[j].size()-same[i][j]*tab[j].size()-same[j][i]*tab[i].size()+same[i][j]*same[j][i];//容斥原理
            }
        }

        return res;
    }
};