
【模拟】兼具大小写的最好英文字母
题目
给你一个由英文字母组成的字符串 s ,请你找出并返回 s 中的 最好 英文字母。返回的字母必须为大写形式。如果不存在满足条件的字母,则返回一个空字符串。
最好 英文字母的大写和小写形式必须 都 在 s 中出现。
英文字母 b 比另一个英文字母 a 更好 的前提是:英文字母表中,b 在 a 之 后 出现。
示例 1:
1
2
3
4
| 输入:s = "lEeTcOdE"
输出:"E"
解释:
字母 'E' 是唯一一个大写和小写形式都出现的字母。
|
示例 2:
1
2
3
4
5
| 输入:s = "arRAzFif"
输出:"R"
解释:
字母 'R' 是大写和小写形式都出现的最好英文字母。
注意 'A' 和 'F' 的大写和小写形式也都出现了,但是 'R' 比 'F' 和 'A' 更好。
|
示例 3:
1
2
3
4
| 输入:s = "AbCdEfGhIjK"
输出:""
解释:
不存在大写和小写形式都出现的字母。
|
提示:
1 <= s.length <= 1000s 由小写和大写英文字母组成
解题思路
按题意模拟即可。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public:
string greatestLetter(string s) {
vector<int> a(26,0),A(26,0);
for(auto &x: s){
if(islower(x)) a[x-'a']++;
else A[x-'A']++;
}
string res;
for(int i=25;i>=0;i--){
if(a[i]&&A[i]) {
res += 'A'+i;
break;
}
}
return res;
}
};
|
【枚举+数学】个位数字为 K 的整数之和
题目
给你两个整数 num 和 k ,考虑具有以下属性的正整数多重集:
- 每个整数个位数字都是
k 。 - 所有整数之和是
num 。
返回该多重集的最小大小,如果不存在这样的多重集,返回 -1 。
注意:
- 多重集与集合类似,但多重集可以包含多个同一整数,空多重集的和为
0 。 - 个位数字 是数字最右边的数位。
示例 1:
1
2
3
4
5
6
| 输入:num = 58, k = 9
输出:2
解释:
多重集 [9,49] 满足题目条件,和为 58 且每个整数的个位数字是 9 。
另一个满足条件的多重集是 [19,39] 。
可以证明 2 是满足题目条件的多重集的最小长度。
|
示例 2:
1
2
3
| 输入:num = 37, k = 2
输出:-1
解释:个位数字为 2 的整数无法相加得到 37 。
|
示例 3:
1
2
3
| 输入:num = 0, k = 7
输出:0
解释:空多重集的和为 0 。
|
提示:
0 <= num <= 30000 <= k <= 9
解题思路
构造题的感觉
考虑若干个末位数字相加后,其和的个位数字能否和num的个位数字相同
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution {
public:
int minimumNumbers(int num, int k) {
if(num==0) return 0;
if(num<k) return -1;
int tar = num%10;
bool flag = false;
for(int i=1;i<=10;i++){
if(k*i%10==tar && i*k<=num){
return i;
flag=true;
}
}
return -1;
}
};
|
【贪心】小于等于 K 的最长二进制子序列
题目
给你一个二进制字符串 s 和一个正整数 k 。
请你返回 s 的 最长 子序列,且该子序列对应的 二进制 数字小于等于 k 。
注意:
- 子序列可以有 前导 0 。
- 空字符串视为
0 。 - 子序列 是指从一个字符串中删除零个或者多个字符后,不改变顺序得到的剩余字符序列。
示例 1:
1
2
3
4
5
| 输入:s = "1001010", k = 5
输出:5
解释:s 中小于等于 5 的最长子序列是 "00010" ,对应的十进制数字是 2 。
注意 "00100" 和 "00101" 也是可行的最长子序列,十进制分别对应 4 和 5 。
最长子序列的长度为 5 ,所以返回 5 。
|
示例 2:
1
2
3
4
| 输入:s = "00101001", k = 1
输出:6
解释:"000001" 是 s 中小于等于 1 的最长子序列,对应的十进制数字是 1 。
最长子序列的长度为 6 ,所以返回 6 。
|
提示:
1 <= s.length <= 1000s[i] 要么是 '0' ,要么是 '1' 。1 <= k <= 109
解题思路
赛时想到的是二分+贪心,但是贪心贪错了
补题的时候想到了正确的贪心方式,二分就没必要了
考虑k的二进制表示,其位数为len,(最高位为1)
那么二进制位数小于len(最高位为1,即不考虑前导0)的数一定小于k
如果位数相等,那么可以转换成10进制再比较大小
最后补上尽量多的前导0即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
int longestSubsequence(string s, int k) {
vector<int> tar(1005,0);
int high=-1;
for(int i=0;i<32;i++){
tar[i] = (k>>i)&1;
if(tar[i]==1){
high=i;//k的二进制表示中,最高位1所在的位置
}
}
if(high+1>=s.size()) return s.size();
int n=s.size();
int cnt=0;
reverse(s.begin(),s.end());
for(int i=high+1;i<n;i++){
if(s[i]=='0') cnt++;
}
string suf=s.substr(0,high+1);
reverse(suf.begin(),suf.end());
int cur=stoi(suf,nullptr,2);//将字符串suf中的数看做是二进制编码,转成10进制整数。
if(s[high]=='0') return high+1+cnt;
else if(cur<=k) return high+1+cnt;
else return high+cnt;
}
};
|
【DP】卖木头块
题目
给你两个整数 m 和 n ,分别表示一块矩形木块的高和宽。同时给你一个二维整数数组 prices ,其中 prices[i] = [hi, wi, pricei] 表示你可以以 pricei 元的价格卖一块高为 hi 宽为 wi 的矩形木块。
每一次操作中,你必须按下述方式之一执行切割操作,以得到两块更小的矩形木块:
- 沿垂直方向按高度 完全 切割木块,或
- 沿水平方向按宽度 完全 切割木块
在将一块木块切成若干小木块后,你可以根据 prices 卖木块。你可以卖多块同样尺寸的木块。你不需要将所有小木块都卖出去。你 不能 旋转切好后木块的高和宽。
请你返回切割一块大小为 m x n 的木块后,能得到的 最多 钱数。
注意你可以切割木块任意次。
示例 1:
1
2
3
4
5
6
7
8
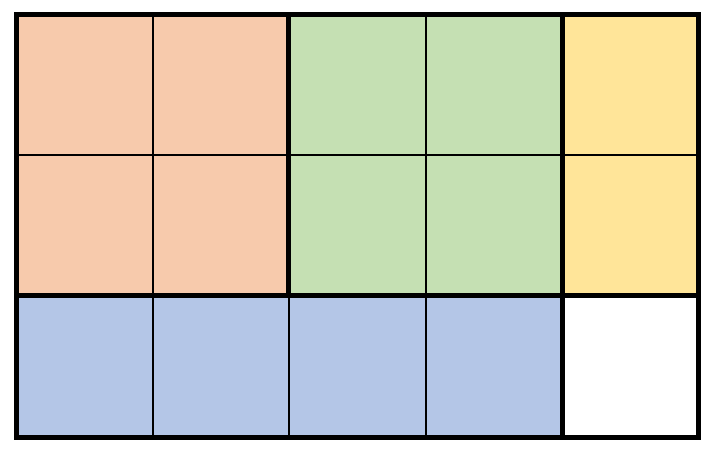
| 输入:m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
输出:19
解释:上图展示了一个可行的方案。包括:
- 2 块 2 x 2 的小木块,售出 2 * 7 = 14 元。
- 1 块 2 x 1 的小木块,售出 1 * 3 = 3 元。
- 1 块 1 x 4 的小木块,售出 1 * 2 = 2 元。
总共售出 14 + 3 + 2 = 19 元。
19 元是最多能得到的钱数。
|
示例 2:
1
2
3
4
5
6
7
8
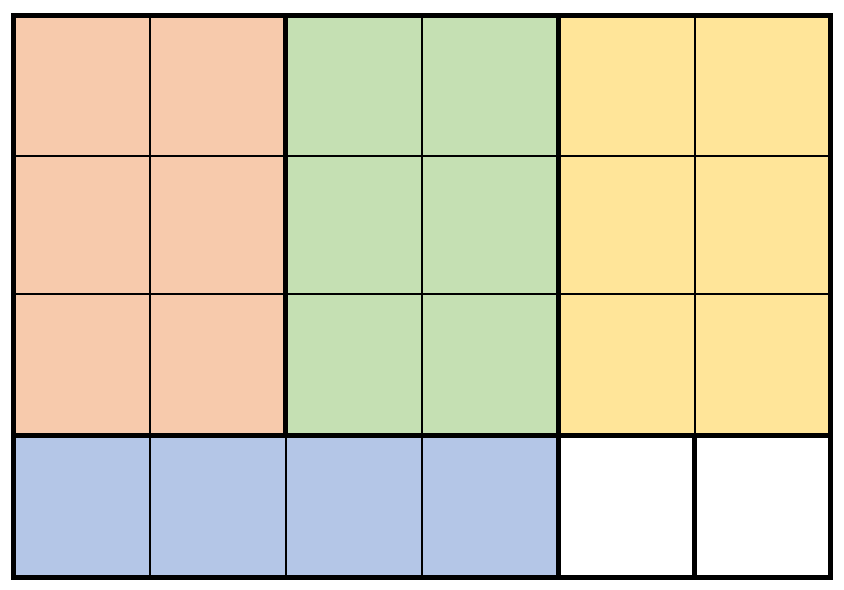
| 输入:m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
输出:32
解释:上图展示了一个可行的方案。包括:
- 3 块 3 x 2 的小木块,售出 3 * 10 = 30 元。
- 1 块 1 x 4 的小木块,售出 1 * 2 = 2 元。
总共售出 30 + 2 = 32 元。
32 元是最多能得到的钱数。
注意我们不能旋转 1 x 4 的木块来得到 4 x 1 的木块。
|
提示:
1 <= m, n <= 2001 <= prices.length <= 2 * 10^4prices[i].length == 31 <= hi <= m1 <= wi <= n1 <= pricei <= 10^6- 所有
(hi, wi) 互不相同 。
解题思路
一眼DP,可惜没时间做
看清题意,切割操作有两种,要么沿水平方向切割,要么沿竖直方向切割
二维vector初始化比起用memset初始化费时地多
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public:
long long sellingWood(int n, int m, vector<vector<int>>& prices) {
// 记录直接卖的收益
vector<vector<int>> A;
A.resize(n + 1, vector<int>(m + 1));
for (auto &vec : prices) A[vec[0]][vec[1]] = vec[2];
vector<vector<long long>> f;
f.resize(n + 1, vector<long long>(m + 1));
for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) {
// 直接卖
f[i][j] = A[i][j];
// 沿水平方向分割
for (int k = 1; k < i; k++) f[i][j] = max(f[i][j], f[k][j] + f[i - k][j]);
// 沿垂直方向分割
for (int k = 1; k < j; k++) f[i][j] = max(f[i][j], f[i][k] + f[i][j - k]);
}
return f[n][m];
}
};
// 作者:TsReaper
// 链接:https://leetcode.cn/circle/discuss/qovhgl/view/OGIKuU/
// 来源:力扣(LeetCode)
// 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
|
记忆化搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #define ll long long
class Solution {
public:
long long sellingWood(int m, int n, vector<vector<int>>& prices) {
long long dp[202][202],single[202][202];
memset(dp,-1,sizeof(dp));
memset(single,0,sizeof(single));
//dp[i][j] 高为i,宽为j的矩形木块 切割后能得到的最多钱数
for(auto &sub : prices){
single[sub[0]][sub[1]] = sub[2];
}
function<ll(int,int)> dfs=[&](int x, int y){
if(dp[x][y]!=-1) return dp[x][y];
if(!x||!y) return 1ll*0;
ll res = single[x][y];
for(int i=1;i<x;i++){
res=max(res,dfs(i,y)+dfs(x-i,y));
}
for(int j=1;j<y;j++){
res=max(res,dfs(x,j)+dfs(x,y-j));
}
dp[x][y]=res;
return dp[x][y];
};
dfs(m,n);
return dp[m][n];
}
};
|



