LeetCode第299场周赛总结

# 【模拟】判断矩阵是否是一个 X 矩阵

# 题目

如果一个正方形矩阵满足下述全部条件，则称之为一个 X 矩阵 ：

矩阵对角线上的所有元素都 不是 0
矩阵中所有其他元素都是 0

给你一个大小为 n x n 的二维整数数组 grid ，表示一个正方形矩阵。如果 grid 是一个 X 矩阵 ，返回 true ；否则，返回 false 。

示例 1：

1
2
3
4
5
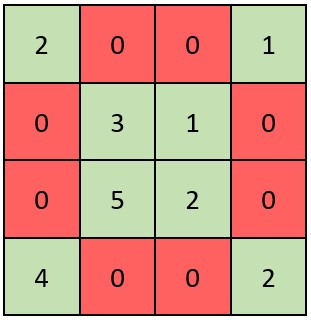
输入：grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
输出：true
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 是一个 X 矩阵。

示例 2：

1
2
3
4
5
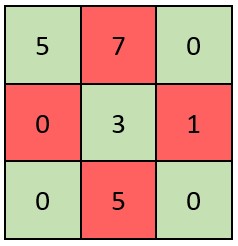
输入：grid = [[5,7,0],[0,3,1],[0,5,0]]
输出：false
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 不是一个 X 矩阵。

提示：

n == grid.length == grid[i].length
3 <= n <= 100
0 <= grid[i][j] <= 10^5

# 解题思路

简单模拟即可

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
public:
    bool checkXMatrix(vector<vector<int>>& grid) {
        int n = grid.size();
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                if(i==j||i+j==n-1){
                    if(grid[i][j]==0) return false;
                }
                else if(grid[i][j]!=0) return false;
            }
        }
        return true;
    }
};

# 【DP】统计放置房子的方式数

# 题目

一条街道上共有 n * 2 个地块，街道的两侧各有 n 个地块。每一边的地块都按从 1 到 n 编号。每个地块上都可以放置一所房子。

现要求街道同一侧不能存在两所房子相邻的情况，请你计算并返回放置房屋的方式数目。由于答案可能很大，需要对 10^9 + 7 取余后再返回。

注意，如果一所房子放置在这条街某一侧上的第 i 个地块，不影响在另一侧的第 i 个地块放置房子。

示例 1：

1
2
3
4
5
6
7
8
输入：n = 1
输出：4
解释：
可能的放置方式：
1. 所有地块都不放置房子。
2. 一所房子放在街道的某一侧。
3. 一所房子放在街道的另一侧。
4. 放置两所房子，街道两侧各放置一所。

示例 2：

1
2
3
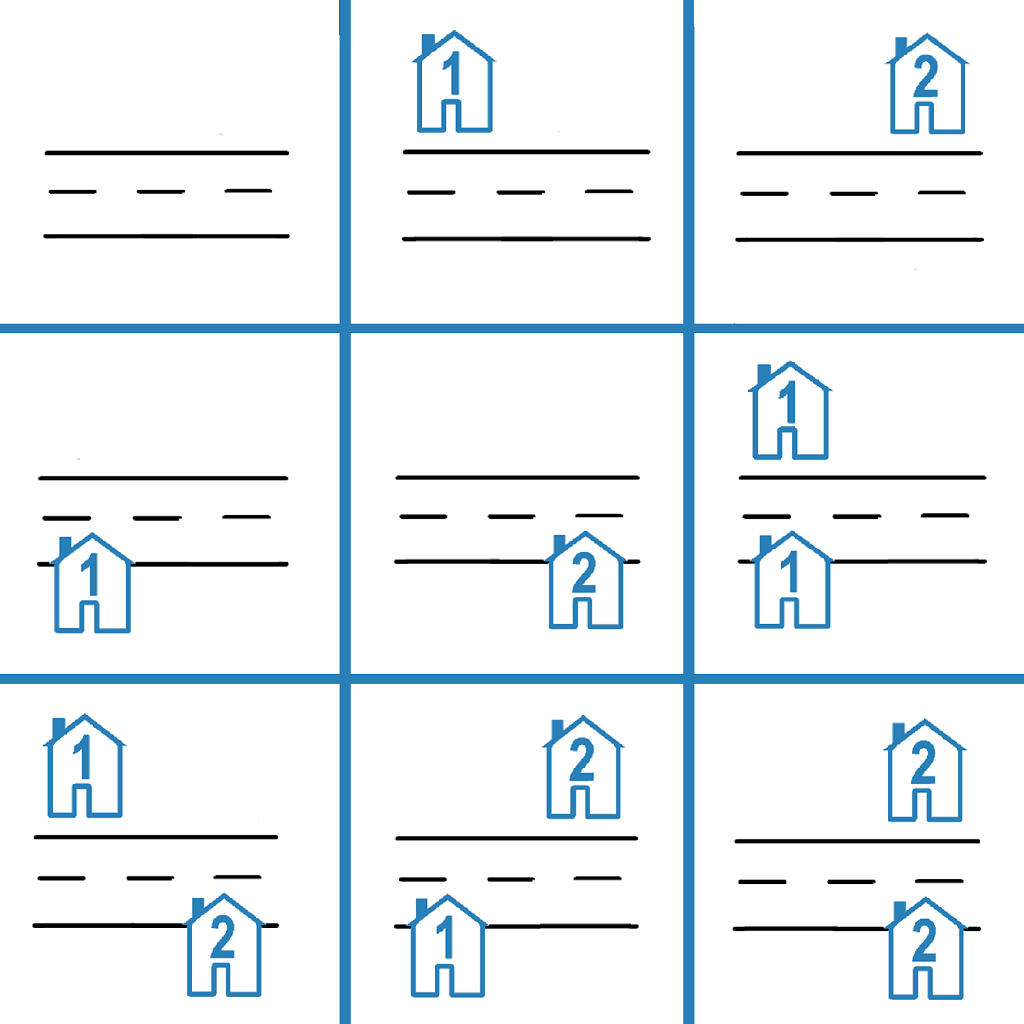
输入：n = 2
输出：9
解释：如上图所示，共有 9 种可能的放置方式。

提示：

1 <= n <= 10^4

# 解题思路

一眼DP，赛时用了三维，dp[i, j, k]表示前i块地，两侧的最后一块是否放置房子的方案数

WA了一发是因为dp数组定义忘记用long long 了

其实只需要考虑一侧就好，因为两侧放置房子是独立的，方案数相同，由乘法原理最后计数相乘即可

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#define ll long long
const int MOD=1e9+7;
class Solution {
public:
    int countHousePlacements(int n) {
        ll dp[n+1][2][2];
        memset(dp,0,sizeof(dp));
        dp[1][0][0]=1;
        dp[1][0][1]=1;
        dp[1][1][0]=1;
        dp[1][1][1]=1;
        for(int i=2;i<=n;i++){
            dp[i][0][0] = (dp[i-1][0][0]+dp[i-1][0][1]+dp[i-1][1][0]+dp[i-1][1][1])%MOD;
            dp[i][0][1] = (dp[i-1][0][0]+dp[i-1][1][0])%MOD;
            dp[i][1][0] = (dp[i-1][0][0]+dp[i-1][0][1])%MOD;
            dp[i][1][1] = (dp[i-1][0][0])%MOD;
        }
        ll res=0;
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                res = (res+dp[n][i][j])%MOD;
            }
        }
        return res;
    }
};

# 偷学代码

令f[i]表示一侧前i块地放置放置房子的方案数，第i块可以放，也可以不放

考虑第i块：1）如果不放房子，那么第i-1块土地可放可不放，加上f[i-1] ； 2）如果放房子，那么第i-1块土地必不可放，第i-2块土地可放可不放，加上f[i-2]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
const int MOD = 1e9 + 7, MX = 1e4 + 1;
int f[MX] = {1, 2};
int init = []() {
    for (int i = 2; i < MX; ++i)
        f[i] = (f[i - 1] + f[i - 2]) % MOD;
    return 0;
}();

class Solution {
public:
    int countHousePlacements(int n) {
        return (long) f[n] * f[n] % MOD;
    }
};

# 【DP】拼接数组的最大分数

# 题目

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，长度都是 n 。

你可以选择两个整数 left 和 right ，其中 0 <= left <= right < n ，接着交换两个子数组 nums1[left...right] 和 nums2[left...right] 。

例如，设 nums1 = [1,2,3,4,5] 和 nums2 = [11,12,13,14,15] ，整数选择 left = 1 和 right = 2，那么 nums1 会变为 [1,12,13,4,5] 而 nums2 会变为 [11,2,3,14,15] 。

你可以选择执行上述操作一次或不执行任何操作。

数组的分数取 sum(nums1) 和 sum(nums2) 中的最大值，其中 sum(arr) 是数组 arr 中所有元素之和。

返回 可能的最大分数 。

子数组 是数组中连续的一个元素序列。arr[left...right] 表示子数组包含 nums 中下标 left 和 right 之间的元素 （含下标 left 和 right 对应元素）。

示例 1：

1
2
3
4
输入：nums1 = [60,60,60], nums2 = [10,90,10]
输出：210
解释：选择 left = 1 和 right = 1 ，得到 nums1 = [60,90,60] 和 nums2 = [10,60,10] 。
分数为 max(sum(nums1), sum(nums2)) = max(210, 80) = 210 。

示例 2：

1
2
3
4
输入：nums1 = [20,40,20,70,30], nums2 = [50,20,50,40,20]
输出：220
解释：选择 left = 3 和 right = 4 ，得到 nums1 = [20,40,20,40,20] 和 nums2 = [50,20,50,70,30] 。
分数为 max(sum(nums1), sum(nums2)) = max(140, 220) = 220 。

示例 3：

1
2
3
4
输入：nums1 = [7,11,13], nums2 = [1,1,1]
输出：31
解释：选择不交换任何子数组。
分数为 max(sum(nums1), sum(nums2)) = max(31, 3) = 31 。

提示：

n == nums1.length == nums2.length
1 <= n <= 10^5
1 <= nums1[i], nums2[i] <= 10^4

# 解题思路

交换两个数组的同一段的区间和，使得单个数组的总和最大

在草稿纸上推一下示例就可以发现，就是找两个数组的差值数组的最大连续子段和，交换两个数组的这一段即可

WA了一次是因为，两个数组的差值数组要考虑两种情况，a-b和b-a，只考虑了一种

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#define ll long long
class Solution {
public:
    int maximumsSplicedArray(vector<int>& nums1, vector<int>& nums2) {
        int n=nums1.size();
        vector<int> sum1(n+1,0),sum2(n+1,0);
        for(int i=1;i<=n;i++){
            sum1[i]=sum1[i-1]+nums1[i-1];
            sum2[i]=sum2[i-1]+nums2[i-1];
        }
       
        vector<int> a1(n+1,0),a2(n+1,0);
        for(int i=1;i<=n;i++){
            a1[i] = nums2[i-1]-nums1[i-1];
            a2[i] = nums1[i-1]-nums2[i-1];
            // cout<<a[i]<<' ';
        }
        int maxv1=0,cur=0;
        for(int i=1;i<=n;i++){
            cur = max(a1[i],cur+a1[i]);
            maxv1=max(maxv1,cur);
        }
        int maxv2=0;
        cur=0;
        for(int i=1;i<=n;i++){
            cur = max(a2[i],cur+a2[i]);
            maxv2=max(maxv2,cur);
        }
        int res = max(sum1[n]+maxv1,sum2[n]+maxv2);
        return res;
    }
};

# 【DFS序+枚举】从树中删除边的最小分数

# 题目

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点，以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。

删除树中两条不同的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

分别获取三个组件每个组件中所有节点值的异或值。
最大异或值和最小异或值的差值就是这一种删除边方案的分数。

例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = ***6***、1 ^ 9 = ***8*** 和 3 ^ 3 ^ 3 = ***3*** 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。

返回在给定树上执行任意删除边方案可能的最小分数。

示例 1：

1
2
3
4
5
6
7
8
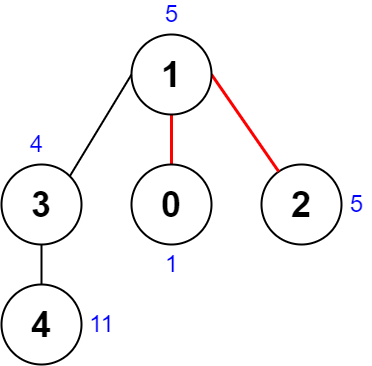
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出：9
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ，值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ，值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ，值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值，10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。

示例 2：

1
2
3
4
5
6
7
8
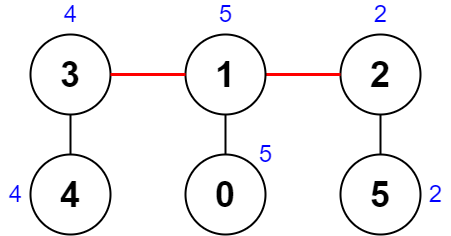
输入：nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出：0
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [3,4] ，值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ，值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ，值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值，0 - 0 = 0 。
无法获得比 0 更小的分数 0 。

提示：

n == nums.length
3 <= n <= 1000
1 <= nums[i] <= 10^8
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
edges 表示一棵有效的树

# 解题思路

$O(n^2)$ 时间内枚举删除的两条边，$O(1)$ 时间内计算子树的异或和

注意到 $a\oplus b \oplus a=b$

删除两条边后有不同的情况，需要分类讨论：删除的两条边对应的4个（或3个）是否存在祖先关系

利用DFS序在O(1)时间内判断两点是否存在祖先关系

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
const int INF=0x3f3f3f3f;
class Solution {
public:
    int minimumScore(vector<int>& nums, vector<vector<int>>& edges) {
        int n = nums.size();
        vector<int> G[n];
        for(auto &x: edges){
            G[x[0]].push_back(x[1]);
            G[x[1]].push_back(x[0]);
        }
        
        vector<int> vis(n,0),in(n,0),out(n,0),val(n,0);
        int time=0;
        function<int(int)> dfs = [&](int u)->int{
            in[u] = ++time;
            val[u] = nums[u];
            vis[u] = 1;
            for(auto &v: G[u]){
                if(vis[v]) continue;
                vis[v]=1;
                val[u] = val[u]^dfs(v);
            }
            out[u] = time;
            return val[u];
        };
        int root = 1;
        dfs(root);
       
        auto isFather = [&](int u, int v)->bool{
            return in[u]<=in[v] && out[u]>=out[v];  
        };

        for(auto &x: edges){//枚举边的时候确保第0个元素是第1个元素的父节点
            if(isFather(x[0],x[1])) continue;
            else swap(x[0],x[1]);
        }
        

        int maxv,minv,res=INF;
        for(int i=0;i<edges.size();i++){//枚举删除第1条变
            int xi=edges[i][0],yi=edges[i][1];
            for(int j=0;j<i;j++){//枚举删除第2条边
                int xj=edges[j][0],yj=edges[j][1];
                if(isFather(yi,yj)){//yi是yj的父节点
                    maxv = max({val[yj],val[yi]^val[yj],val[root]^val[yi]});
                    minv = min({val[yj],val[yi]^val[yj],val[root]^val[yi]});
                }else if(isFather(yj,yi)){//yj是yi的父节点
                    maxv = max({val[yi],val[yj]^val[yi],val[root]^val[yj]});
                    minv = min({val[yi],val[yj]^val[yi],val[root]^val[yj]});
                }else{//不存在祖先关系
                    maxv = max({val[yi],val[yj],val[root]^val[yi]^val[yj]});
                    minv = min({val[yi],val[yj],val[root]^val[yi]^val[yj]});
                }
                res = min(maxv-minv,res);
            }
        }
        return res;
    }
};