
【思维】使数组中所有元素都等于零
题目
给你一个非负整数数组 nums 。在一步操作中,你必须:
- 选出一个正整数
x ,x 需要小于或等于 nums 中 最小 的 非零 元素。 nums 中的每个正整数都减去 x。
返回使 nums 中所有元素都等于 0 需要的 最少 操作数。
示例 1:
1
2
3
4
5
6
| 输入:nums = [1,5,0,3,5]
输出:3
解释:
第一步操作:选出 x = 1 ,之后 nums = [0,4,0,2,4] 。
第二步操作:选出 x = 2 ,之后 nums = [0,2,0,0,2] 。
第三步操作:选出 x = 2 ,之后 nums = [0,0,0,0,0] 。
|
示例 2:
1
2
3
| 输入:nums = [0]
输出:0
解释:nums 中的每个元素都已经是 0 ,所以不需要执行任何操作。
|
提示:
1 <= nums.length <= 1000 <= nums[i] <= 100
解题思路
可以想到,对数组进行排序后,一次操作能使最小的那些数归0
所以本质上是求数组中非不同非零数的个数
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public:
int minimumOperations(vector<int>& nums) {
int n = nums.size();
vector<int> a(101,0);
for(auto &x: nums){
if(x>0) a[x]++;
}
int res=0;
for(int i=1;i<=100;i++) {
if(a[i]) res++;
}
return res;
}
};
|
【贪心】分组的最大数量
题目
给你一个正整数数组 grades ,表示大学中一些学生的成绩。你打算将 所有 学生分为一些 有序 的非空分组,其中分组间的顺序满足以下全部条件:
- 第
i 个分组中的学生总成绩 小于 第 (i + 1) 个分组中的学生总成绩,对所有组均成立(除了最后一组)。 - 第
i 个分组中的学生总数 小于 第 (i + 1) 个分组中的学生总数,对所有组均成立(除了最后一组)。
返回可以形成的 最大 组数。
示例 1:
1
2
3
4
5
6
7
| 输入:grades = [10,6,12,7,3,5]
输出:3
解释:下面是形成 3 个分组的一种可行方法:
- 第 1 个分组的学生成绩为 grades = [12] ,总成绩:12 ,学生数:1
- 第 2 个分组的学生成绩为 grades = [6,7] ,总成绩:6 + 7 = 13 ,学生数:2
- 第 3 个分组的学生成绩为 grades = [10,3,5] ,总成绩:10 + 3 + 5 = 18 ,学生数:3
可以证明无法形成超过 3 个分组。
|
示例 2:
1
2
3
| 输入:grades = [8,8]
输出:1
解释:只能形成 1 个分组,因为如果要形成 2 个分组的话,会导致每个分组中的学生数目相等。
|
提示:
1 <= grades.length <= 10^51 <= grades[i] <= 10^5
解题思路
为了使组数最大,应该按这样的大小分: 1,2,3….,n
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
int maximumGroups(vector<int>& grades) {
int n = grades.size();
int tmp=0,maxv=0;
for(int i=1;;i++){
tmp+=i;
if(tmp>n){
maxv = i-1;
break;
}
}
// cout<<maxv<<endl;
// sort(grades.begin(),grades.end());
return maxv;
}
};
|
【无权值有向图最短距离】找到离给定两个节点最近的节点
题目
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,每个节点 至多 有一条出边。
有向图用大小为 n 下标从 0 开始的数组 edges 表示,表示节点 i 有一条有向边指向 edges[i] 。如果节点 i 没有出边,那么 edges[i] == -1 。
同时给你两个节点 node1 和 node2 。
请你返回一个从 node1 和 node2 都能到达节点的编号,使节点 node1 和节点 node2 到这个节点的距离 较大值最小化。如果有多个答案,请返回 最小 的节点编号。如果答案不存在,返回 -1 。
注意 edges 可能包含环。
示例 1:
1
2
3
4
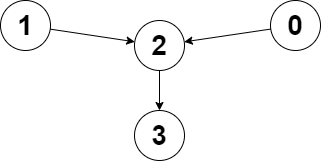
| 输入:edges = [2,2,3,-1], node1 = 0, node2 = 1
输出:2
解释:从节点 0 到节点 2 的距离为 1 ,从节点 1 到节点 2 的距离为 1 。
两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值,所以我们返回节点 2 。
|
示例 2:
1
2
3
4
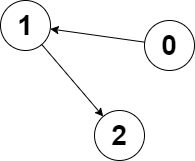
| 输入:edges = [1,2,-1], node1 = 0, node2 = 2
输出:2
解释:节点 0 到节点 2 的距离为 2 ,节点 2 到它自己的距离为 0 。
两个距离的较大值为 2 。我们无法得到一个比 2 更小的较大值,所以我们返回节点 2 。
|
提示:
n == edges.length2 <= n <= 10^5-1 <= edges[i] < nedges[i] != i0 <= node1, node2 < n
解题思路
每个节点至多有一条出边。边无权值,可利用BFS预先处理出到两个root的最短距离,然后遍历找最值即可。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public:
int n;
vector<int> fun(vector<int>& edges, int root){
vector<int> dis(n,-1);
queue<int> que;
que.push(root);
dis[root]=0;
while(!que.empty()){
int u = que.front();
que.pop();
int v = edges[u];
if(v!=-1 && dis[v]==-1){
que.push(v);
dis[v] = dis[u]+1;
}
}
return dis;
}
int closestMeetingNode(vector<int>& edges, int node1, int node2) {
n = edges.size();
vector<int> d1 = fun(edges,node1);
vector<int> d2 = fun(edges,node2);
int minv = INT_MAX;
int res=-1;
for(int i=0;i<n;i++){
if(d1[i]>=0 && d2[i]>=0){
int tmp = max(d1[i],d2[i]);
if(tmp<minv){
minv = tmp;
res = i;
}
}
}
return res;
}
};
|
【有向图最长环】图中的最长环
题目
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示,节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边,那么 edges[i] == -1 。
请你返回图中的 最长 环,如果没有任何环,请返回 -1 。
一个环指的是起点和终点是 同一个 节点的路径。
示例 1:
1
2
3
4
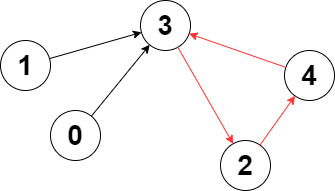
| 输入:edges = [3,3,4,2,3]
输出去:3
解释:图中的最长环是:2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ,所以返回 3 。
|
示例 2:
1
2
3
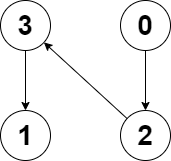
| 输入:edges = [2,-1,3,1]
输出:-1
解释:图中没有任何环。
|
提示:
n == edges.length2 <= n <= 10^5-1 <= edges[i] < nedges[i] != i
拓扑排序找环
每个节点至多有一条出边,所以一个点最多在一个环内。先利用拓扑排序将不成环的点剔除掉,再找最长环。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public:
int longestCycle(vector<int>& edges) {
int n = edges.size();
vector<int> in(n,0),cycle(n,1);
for(auto &x:edges) if(x>-1) in[x]++;
vector<int> zero;
for(int i=0;i<n;i++){
if(in[i]==0) zero.push_back(i);
}
while(!zero.empty()){
int u = zero.back();
zero.pop_back();
cycle[u] = 0;
if(edges[u]>-1){
if(--in[edges[u]]==0) zero.push_back(edges[u]);
}
}
int res = -1;
for(int i=0;i<n;i++){
if(!cycle[i]) continue;
int u = i, cur = 0;
while(cycle[u]){
cur++;
cycle[u] = 0;
u = edges[u];
}
res = max(res, cur);
}
return res;
}
};
|
时间戳
具体来说,初始时间戳clock=1,首次访问一个点 x 时,记录访问这个点的时间 time[x]=clock,然后将 clock 加一。
如果首次访问一个点,则记录当前时间startTime=clock,并尝试从这个点出发,看能否找到环。如果找到了一个之前访问过的点 x,且之前访问 xx 的时间不早于 startTime,则说明我们找到了一个新的环,此时的环长就是前后两次访问 x 的时间差,即 clock−time[x]。
取所有环长的最大值作为答案。若没有找到环,则返回 −1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public:
int longestCycle(vector<int> &edges) {
int n = edges.size(), time[n], ans = -1;
memset(time, 0, sizeof(time));
for (int i = 0, clock = 1; i < n; ++i) {
if (time[i]) continue;
for (int x = i, start_time = clock; x >= 0; x = edges[x]) {
if (time[x]) { // 重复访问
if (time[x] >= start_time) // 找到了一个新的环
ans = max(ans, clock - time[x]);
break;
}
time[x] = clock++;
}
}
return ans;
}
};
|





