Featured image of post LeetCode第305场周赛总结
leetcode contest

LeetCode第305场周赛总结

510/7465

image-20220812102203754

【枚举】算术三元组的数目

题目

给你一个下标从 0 开始、严格递增 的整数数组 nums 和一个正整数 diff 。如果满足下述全部条件，则三元组 (i, j, k) 就是一个 算术三元组 ：

  • i < j < k ，
  • nums[j] - nums[i] == diff 且
  • nums[k] - nums[j] == diff

返回不同 算术三元组 的数目*。*

示例 1：

1
2
3
4
5

输入：nums = [0,1,4,6,7,10], diff = 3
输出：2
解释：
(1, 2, 4) 是算术三元组：7 - 4 == 3 且 4 - 1 == 3 。
(2, 4, 5) 是算术三元组：10 - 7 == 3 且 7 - 4 == 3 。

示例 2：

1
2
3
4
5

输入：nums = [4,5,6,7,8,9], diff = 2
输出：2
解释：
(0, 2, 4) 是算术三元组：8 - 6 == 2 且 6 - 4 == 2 。
(1, 3, 5) 是算术三元组：9 - 7 == 2 且 7 - 5 == 2 。

提示：

  • 3 <= nums.length <= 200
  • 0 <= nums[i] <= 200
  • 1 <= diff <= 50
  • nums 严格 递增

解题思路

看到数据范围很小，直接就三层循环走起了

其实可以利用单调性，一次遍历即可

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
public:
    int arithmeticTriplets(vector<int>& nums, int diff) {
        int n = nums.size();
        int res=0;
        
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                for(int k=0;k<n;k++){
                    if(i<j && j<k && nums[j]-nums[i]==diff && nums[k]-nums[j]==diff) res++;
                }
            }
        }
        return res;
    }
};

偷学代码

1
2
3
4
5
6
7
8
9

class Solution {
public:
    int arithmeticTriplets(vector<int>& nums, int diff) {
        set<int>s(nums.begin(),nums.end());
        int ret=0;
        for(int i:s)ret+=(s.count(i-diff)&&s.count(i+diff));
        return ret;
    }
};

【DFS/BFS/并查集】受限条件下可到达节点的数目

题目

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目*。*

注意，节点 0 不 会标记为受限节点。

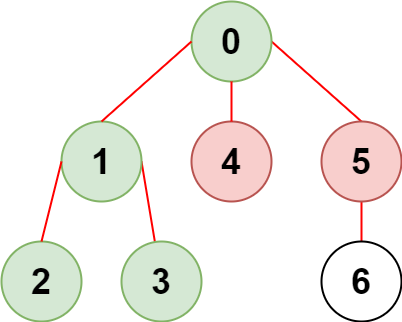
示例 1：

img

1
2
3
4

输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出：4
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。

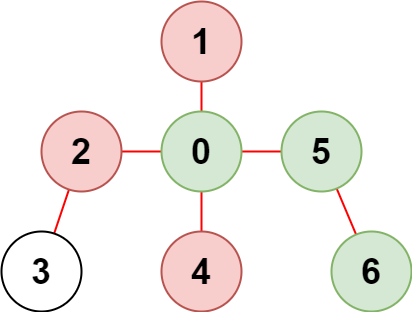
示例 2：

img

1
2
3
4

输入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
输出：3
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,5,6] 可以从节点 0 到达。

提示：

  • 2 <= n <= 10^5
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • edges 表示一棵有效的树
  • 1 <= restricted.length < n
  • 1 <= restricted[i] < n
  • restricted 中的所有值 互不相同

解题思路

常规搜索，DFS/BFS均可

也可以用并查集

代码

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
public:
    int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
        vector<int> G[n];
        for(auto &x: edges){
            G[x[0]].push_back(x[1]);
            G[x[1]].push_back(x[0]);
        }
        vector<int> restr(n,0);
        for(auto &x: restricted){
            restr[x] = 1;
        }
        vector<int> dis(n,-1);
        dis[0] = 0;
        queue<pair<int,int>> que;
        que.emplace(0,0);
        while(!que.empty()){
            auto [u,d] = que.front();
            que.pop();
            for(auto &v: G[u]){
                if(dis[v]>-1) continue;
                if(restr[v]) continue;
                dis[v] = d+1;
                que.emplace(v,dis[v]);
            }
        }
        int res=0;
        for(int i=0;i<n;i++){
            if(dis[i]>-1) res++;
        }
        return res;
    }
};

并查集

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

const int MAXN = 1e5+5;
int fa[MAXN],sz[MAXN];
int find(int x){
    return x==fa[x]?x:(fa[x]=find(fa[x]));
}
void join(int x, int y){
    int a = find(x);
    int b = find(y);
    if(a!=b){
        if(sz[a]<sz[b]) swap(a,b);
        fa[b] = a;
        sz[a] += sz[b];
    }
}
class Solution {
public:
    int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
        for(int i=0;i<n;i++){
            fa[i] = i;
            sz[i] = 1;
        }
        vector<int> ban(n,0);
        for(auto &x: restricted) ban[x]=1;
        for(auto &vec: edges){
            int u = vec[0], v = vec[1];
            if(ban[u] || ban[v]) continue;
            join(u, v);
        }
        // for(int i=0;i<n;i++){
        //     cout<<fa[i]<<' ';
        // }
        return sz[fa[0]];
    }
};

【线性DP】检查数组是否存在有效划分

题目

给你一个下标从 0 开始的整数数组 nums ，你必须将数组划分为一个或多个 连续 子数组。

如果获得的这些子数组中每个都能满足下述条件 之一 ，则可以称其为数组的一种 有效 划分：

  1. 子数组 恰 由 2 个相等元素组成，例如，子数组 [2,2] 。
  2. 子数组 恰 由 3 个相等元素组成，例如，子数组 [4,4,4] 。
  3. 子数组 恰 由 3 个连续递增元素组成，并且相邻元素之间的差值为 1 。例如，子数组 [3,4,5] ，但是子数组 [1,3,5] 不符合要求。

如果数组 至少 存在一种有效划分，返回 true ，否则，返回 false 。

示例 1：

1
2
3
4

输入：nums = [4,4,4,5,6]
输出：true
解释：数组可以划分成子数组 [4,4] 和 [4,5,6] 。
这是一种有效划分，所以返回 true 。

示例 2：

1
2
3

输入：nums = [1,1,1,2]
输出：false
解释：该数组不存在有效划分。

提示：

  • 2 <= nums.length <= 10^5
  • 1 <= nums[i] <= 10^6

解题思路

令dp[i][j]表示前i个数中，状态为j ， 是否有效，其中j=0表示最后两个元素相等，j=1表示最后3个元素相等，j=2表示最后3个元素连续递增且差值为1

按情况讨论即可，很常规的一道线性DP

也可以省略第二维，将3种情况合在一起考虑

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

class Solution {
public:
    bool validPartition(vector<int>& nums) {
        int n = nums.size();
        int dp[n][3];
        memset(dp,0,sizeof(dp));
        
        if(nums[1]==nums[0]) dp[1][0] = 1;
        
        for(int i=2;i<n;i++){
            
            //2个连续
            if(nums[i]!=nums[i-1]) dp[i][0] = 0;
            else{
                if(dp[i-2][0] || dp[i-2][1] || dp[i-2][2]) dp[i][0] = 1;
                else dp[i][0]=0;
            }
            //3个连续相等
            if(nums[i]!=nums[i-1] || nums[i-1]!=nums[i-2]) dp[i][1] = 0;
            else{
                if(i-3<0 || dp[i-3][0] || dp[i-3][1] ||dp[i-3][2]) dp[i][1] = 1;
                else dp[i][1] = 0;
            }
            
            //3个连续递增
            if(nums[i]!=nums[i-1]+1 || nums[i-1]!=nums[i-2]+1) dp[i][2] = 0;
            else{
                if(i-3<0 || dp[i-3][0] || dp[i-3][1] ||dp[i-3][2]) dp[i][2] = 1;
                else dp[i][2] = 0;
            }
            
        }
        
        return dp[n-1][0] || dp[n-1][1] || dp[n-1][2];
        
    }
};

【序列DP】最长理想子序列

题目

给你一个由小写字母组成的字符串 s ，和一个整数 k 。如果满足下述条件，则可以将字符串 t 视作是 理想字符串 ：

  • t 是字符串 s 的一个子序列。
  • t 中每两个 相邻 字母在字母表中位次的绝对差值小于或等于 k 。

返回 最长 理想字符串的长度。

字符串的子序列同样是一个字符串，并且子序列还满足：可以经由其他字符串删除某些字符（也可以不删除）但不改变剩余字符的顺序得到。

**注意：**字母表顺序不会循环。例如，'a' 和 'z' 在字母表中位次的绝对差值是 25 ，而不是 1 。

示例 1：

1
2
3
4

输入：s = "acfgbd", k = 2
输出：4
解释：最长理想字符串是 "acbd" 。该字符串长度为 4 ，所以返回 4 。
注意 "acfgbd" 不是理想字符串，因为 'c' 和 'f' 的字母表位次差值为 3 。

示例 2：

1
2
3

输入：s = "abcd", k = 3
输出：4
解释：最长理想字符串是 "abcd" ，该字符串长度为 4 ，所以返回 4 。

提示：

  • 1 <= s.length <= 10^5
  • 0 <= k <= 25
  • s 由小写英文字母组成

解题思路

令dp[i][j]表示以前i个字符中，且最后一个字符为j+‘a’的最长理想字符串的长度

然后进行状态转移即可，很常规的一道序列DP

WA了一发，直接返回dp[n-1][s.back()-‘a’]了，应该返回max (dp[n-1][j])，j范围为[0,26)的

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
public:
    int longestIdealString(string s, int k) {
        int n = s.size();
        int dp[n][26];
        memset(dp,0,sizeof(dp));
        dp[0][s[0]-'a'] = 1;
        for(int i=1;i<n;i++){
            for(int j=0;j<26;j++){
                dp[i][j] = dp[i-1][j];
            }
            for(int j=0;j<26;j++){
                if(abs(j-(s[i]-'a'))>k) continue;
                dp[i][s[i]-'a'] = max(dp[i][s[i]-'a'], dp[i-1][j]+1);
            }
        }
        int res=0;
        for(int j=0;j<26;j++){
            res = max(res, dp[n-1][j]);
        }
        return res;
    }
};

偷学代码

也可以直接令dp[i]表示以字符i+‘a’结尾的最长理想子序列的长度

省去字符的序号这个维度

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
public:
    int longestIdealString(string s, int k) {
        vector<int> f(26);
        for (char c : s) {
            int x = c - 'a';
            int t = 0;
            for (int y = 0; y < 26; y++) if (abs(x - y) <= k) t = max(t, f[y] + 1);
            f[x] = max(f[x], t);
        }

        int ans = 0;
        for (int i = 0; i < 26; i++) ans = max(ans, f[i]);
        return ans;
    }
};
© 2020 - 2024 おう てつ の blog
Built with Hugo
Theme Stack designed by Jimmy