LeetCode第308场周赛总结

【排序+贪心+前缀和+二分】和有限的最长子序列

题目

给你一个长度为 n 的整数数组 nums ，和一个长度为 m 的整数数组 queries 。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是 nums 中元素之和小于等于 queries[i] 的 子序列 的最大长度。

子序列 是由一个数组删除某些元素（也可以不删除）但不改变剩余元素顺序得到的一个数组。

示例 1：

1
2
3
4
5
6
输入：nums = [4,5,2,1], queries = [3,10,21]
输出：[2,3,4]
解释：queries 对应的 answer 如下：
- 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ，所以 answer[0] = 2 。
- 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ，所以 answer[1] = 3 。
- 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ，所以 answer[2] = 4 。

示例 2：

1
2
3
输入：nums = [2,3,4,5], queries = [1]
输出：[0]
解释：空子序列是唯一一个满足元素和小于或等于 1 的子序列，所以 answer[0] = 0 。

提示：

n == nums.length
m == queries.length
1 <= n, m <= 1000
1 <= nums[i], queries[i] <= 10^6

解题思路

选取子序列，和顺序无关，可以考虑先排序

元素之和小于等于一个数的最大长度，为了选的数更多，肯定先考虑选小的数

求个前缀和

在前缀和数组上找大于queries[i]的第一个位置idx，那么前idx-1个元素是小于等于queries[i]的最大长度

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
public:
    vector<int> answerQueries(vector<int>& nums, vector<int>& queries) {
        int n = nums.size(), m = queries.size();
        vector<long long> sum(n+1,0);
        sort(nums.begin(),nums.end());
        for(int i=1;i<=n;i++) sum[i] = sum[i-1]+nums[i-1];
        vector<int> res;
        for(int i=0;i<m;i++){
            int idx = upper_bound(sum.begin(),sum.end(),queries[i])-sum.begin();
            res.push_back(idx-1);
        }
        return res;
    }
};

【模拟】从字符串中移除星号

题目

给你一个包含若干星号 * 的字符串 s 。

在一步操作中，你可以：

选中 s 中的一个星号。
移除星号左侧最近的那个 非星号 字符，并移除该星号自身。

返回移除所有星号之后的字符串**。**

注意：

生成的输入保证总是可以执行题面中描述的操作。
可以证明结果字符串是唯一的。

示例 1：

1
2
3
4
5
6
7
输入：s = "leet**cod*e"
输出："lecoe"
解释：从左到右执行移除操作：
- 距离第 1 个星号最近的字符是 "leet**cod*e" 中的 't' ，s 变为 "lee*cod*e" 。
- 距离第 2 个星号最近的字符是 "lee*cod*e" 中的 'e' ，s 变为 "lecod*e" 。
- 距离第 3 个星号最近的字符是 "lecod*e" 中的 'd' ，s 变为 "lecoe" 。
不存在其他星号，返回 "lecoe" 。

示例 2：

1
2
3
输入：s = "erase*****"
输出：""
解释：整个字符串都会被移除，所以返回空字符串。

提示：

1 <= s.length <= 10^5
s 由小写英文字母和星号 * 组成
s 可以执行上述操作

解题思路

利用栈模拟即可

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    string removeStars(string s) {
        int n = s.size();
        stack<char> stk;
        string res;
        for(int i=0;i<n;i++){
            if(s[i]!='*') stk.push(s[i]);
            else if(!stk.empty()) stk.pop();
        }
        while(!stk.empty()) {
            res+=stk.top();
            stk.pop();
        }
        reverse(res.begin(),res.end());
        return res;
    }
};

【模拟】收集垃圾的最少总时间

题目

给你一个下标从 0 开始的字符串数组 garbage ，其中 garbage[i] 表示第 i 个房子的垃圾集合。garbage[i] 只包含字符 'M' ，'P' 和 'G' ，但可能包含多个相同字符，每个字符分别表示一单位的金属、纸和玻璃。垃圾车收拾一单位的任何一种垃圾都需要花费 1 分钟。

同时给你一个下标从 0 开始的整数数组 travel ，其中 travel[i] 是垃圾车从房子 i 行驶到房子 i + 1 需要的分钟数。

城市里总共有三辆垃圾车，分别收拾三种垃圾。每辆垃圾车都从房子 0 出发，按顺序 到达每一栋房子。但它们 不是必须 到达所有的房子。

任何时刻只有一辆垃圾车处在使用状态。当一辆垃圾车在行驶或者收拾垃圾的时候，另外两辆车不能做任何事情。

请你返回收拾完所有垃圾需要花费的最少总分钟数。

示例 1：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
输入：garbage = ["G","P","GP","GG"], travel = [2,4,3]
输出：21
解释：
收拾纸的垃圾车：
1. 从房子 0 行驶到房子 1
2. 收拾房子 1 的纸垃圾
3. 从房子 1 行驶到房子 2
4. 收拾房子 2 的纸垃圾
收拾纸的垃圾车总共花费 8 分钟收拾完所有的纸垃圾。
收拾玻璃的垃圾车：
1. 收拾房子 0 的玻璃垃圾
2. 从房子 0 行驶到房子 1
3. 从房子 1 行驶到房子 2
4. 收拾房子 2 的玻璃垃圾
5. 从房子 2 行驶到房子 3
6. 收拾房子 3 的玻璃垃圾
收拾玻璃的垃圾车总共花费 13 分钟收拾完所有的玻璃垃圾。
由于没有金属垃圾，收拾金属的垃圾车不需要花费任何时间。
所以总共花费 8 + 13 = 21 分钟收拾完所有垃圾。

示例 2：

1
2
3
4
5
6
7
输入：garbage = ["MMM","PGM","GP"], travel = [3,10]
输出：37
解释：
收拾金属的垃圾车花费 7 分钟收拾完所有的金属垃圾。
收拾纸的垃圾车花费 15 分钟收拾完所有的纸垃圾。
收拾玻璃的垃圾车花费 15 分钟收拾完所有的玻璃垃圾。
总共花费 7 + 15 + 15 = 37 分钟收拾完所有的垃圾。

提示：

2 <= garbage.length <= 10^5
garbage[i] 只包含字母 'M' ，'P' 和 'G' 。
1 <= garbage[i].length <= 10
travel.length == garbage.length - 1
1 <= travel[i] <= 100

解题思路

模拟每辆垃圾车运行的过程，遍历一遍即可。

找到最后打扫的位置。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int garbageCollection(vector<string>& garbage, vector<int>& travel) {
        int n = garbage.size();
        vector<int> res(3,0);
        vector<int> tmp(3,0);
        auto fun = [&](char ch, int k)->void{
            for(int i=0;i<n;i++){
                int cnt=0;
                for(auto &x: garbage[i]) if(x==ch) cnt++;
                if(cnt>0) {
                    tmp[k]+=cnt, res[k]=tmp[k];
                }
                if(i!=n-1) tmp[k] += travel[i];
            }
        };
        fun('G',0);
        fun('P',1);
        fun('M',2);
        return res[0]+res[1]+res[2];
    }
};

【拓扑排序+构造】给定条件下构造矩阵

题目

给你一个正整数 k ，同时给你：

一个大小为 n 的二维整数数组 rowConditions ，其中 rowConditions[i] = [abovei, belowi] 和
一个大小为 m 的二维整数数组 colConditions ，其中 colConditions[i] = [lefti, righti] 。

两个数组里的整数都是 1 到 k 之间的数字。

你需要构造一个 k x k 的矩阵，1 到 k 每个数字需要 恰好出现一次 。剩余的数字都是 0 。

矩阵还需要满足以下条件：

对于所有 0 到 n - 1 之间的下标 i ，数字 abovei 所在的行必须在数字 belowi 所在行的上面。
对于所有 0 到 m - 1 之间的下标 i ，数字 lefti 所在的列必须在数字 righti 所在列的左边。

返回满足上述要求的任意矩阵。如果不存在答案，返回一个空的矩阵。

示例 1：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
输入：k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]]
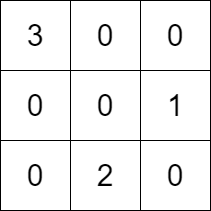
输出：[[3,0,0],[0,0,1],[0,2,0]]
解释：上图为一个符合所有条件的矩阵。
行要求如下：
- 数字 1 在第 1 行，数字 2 在第 2 行，1 在 2 的上面。
- 数字 3 在第 0 行，数字 2 在第 2 行，3 在 2 的上面。
列要求如下：
- 数字 2 在第 1 列，数字 1 在第 2 列，2 在 1 的左边。
- 数字 3 在第 0 列，数字 2 在第 1 列，3 在 2 的左边。
注意，可能有多种正确的答案。

示例 2：

1
2
3
4
输入：k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]]
输出：[]
解释：由前两个条件可以得到 3 在 1 的下面，但第三个条件是 3 在 1 的上面。
没有符合条件的矩阵存在，所以我们返回空矩阵。

提示：

2 <= k <= 400
1 <= rowConditions.length, colConditions.length <= 10^4
rowConditions[i].length == colConditions[i].length == 2
1 <= abovei, belowi, lefti, righti <= k
abovei != belowi
lefti != righti

解题思路

行和列之间没有约束，只有行和行之间，列和列之间有约束

利用拓扑排序找出满足约束的位置

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    int n;
    vector<int> fun(vector<vector<int>>& vec){
        vector<int> G[n+1];
        vector<int> indegree(n+1,0);
        for(auto &x: vec){
            G[x[0]].push_back(x[1]);
            indegree[x[1]]++;
        }
        vector<int> res;
        queue<int> q;
        for(int i=1;i<=n-1;i++) if(indegree[i]==0) q.push(i);
        if(q.empty()) return {};
        while(!q.empty()){
            int u = q.front();
            q.pop();
            res.push_back(u);
            for(auto &v: G[u]){
                if(--indegree[v]==0) q.push(v);
            }
        }

        if(res.size() == n-1) return res;
        return {};
    }
    vector<vector<int>> buildMatrix(int k, vector<vector<int>>& rowConditions, vector<vector<int>>& colConditions) {
        n = k+1;
        vector<int> row = fun(rowConditions);
        vector<int> col = fun(colConditions);
        // for(auto &x: row)  cout<<x<<' ';cout<<endl;
        // for(auto &x: col) cout<<x<<' ';cout<<endl;
        if(row.empty() || col.empty()) return {};
        vector<vector<int>> res(k, vector<int>(k,0));
        vector<int> hang(k+1,0),lie(k+1,0);//数字i 的行 和列
        for(int i=0;i<k;i++){
            hang[row[i]] = i;
        }
        for(int i=0;i<k;i++){
            lie[col[i]] = i;
        }
        for(int i=1;i<=k;i++){
            res[hang[i]][lie[i]] = i;
        }

        return res;
    }
};