Featured image of post LeetCode第311场周赛总结
leetcode contest

LeetCode第311场周赛总结

1355/6710

又掉大分

image-20220924225206563

【简单数学】最小偶倍数

题目

给你一个正整数 n ，返回 2 和 n 的最小公倍数（正整数）。

示例 1：

1
2
3

输入：n = 5
输出：10
解释：5 和 2 的最小公倍数是 10 。

示例 2：

1
2
3

输入：n = 6
输出：6
解释：6 和 2 的最小公倍数是 6 。注意数字会是它自身的倍数。

提示：

  • 1 <= n <= 150

解题思路

最小公倍数 = 总乘积/最大公倍数

代码

1
2
3
4
5
6
7
8

class Solution {
public:
    int smallestEvenMultiple(int n) {
        int all = 2*n;
        int gc = __gcd(2,n);
        return all/gc;
    }
};

【枚举】最长的字母序连续子字符串的长度

题目

字母序连续字符串 是由字母表中连续字母组成的字符串。换句话说，字符串 "abcdefghijklmnopqrstuvwxyz" 的任意子字符串都是 字母序连续字符串 。

  • 例如，"abc" 是一个字母序连续字符串，而 "acb" 和 "za" 不是。

给你一个仅由小写英文字母组成的字符串 s ，返回其 最长 的 字母序连续子字符串 的长度。

示例 1：

1
2
3
4

输入：s = "abacaba"
输出：2
解释：共有 4 个不同的字母序连续子字符串 "a"、"b"、"c" 和 "ab" 。
"ab" 是最长的字母序连续子字符串。

示例 2：

1
2
3

输入：s = "abcde"
输出：5
解释："abcde" 是最长的字母序连续子字符串。

提示：

  • 1 <= s.length <= 10^5
  • s 由小写英文字母组成

解题思路

简单枚举即可，答案最大是26

总能把问题想复杂

WA了一发，忘记i应该从26开始枚举，而不是数组长度

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#include<iostream>
#include<cstring>
using namespace std;

class Solution {
public:
    string str;
    int n;
    bool C(int k){
        bool res = false;
        for(int i=0;i<=n-k;i++){
            int len = 1;
            for(int j=1;j<k;j++){
                if(str[i+j]==str[i+j-1]+1) {len++;}
                else {
                    res = false;
                    break;
                }
            }
            if(len>=k) return true;
        }
        return false;
    }
    int longestContinuousSubstring(string s) {
        str = s;
        n = s.size();
    // cout<<C(26)<<endl;
        for(int i=26;i>=1;i--){
            if(C(i)) return i;
        }

        return 0;
    }
};

偷学代码

这样写不更简单？

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
public:
    int longestContinuousSubstring(string s) {
        int n = s.size();
        int ans = 0;
        for (int i = 0; i < n; i++) {
            int t = 0;
            for (int j = 0; i + j < n; j++) {
                if (s[i + j] - s[i] == j) t++;
                else break;
            }
            ans = max(ans, t);
        }
        return ans;
    }
};

【二叉树的遍历】反转二叉树的奇数层

题目

给你一棵 完美 二叉树的根节点 root ，请你反转这棵树中每个 奇数 层的节点值。

  • 例如，假设第 3 层的节点值是 [2,1,3,4,7,11,29,18] ，那么反转后它应该变成 [18,29,11,7,4,3,1,2] 。

反转后，返回树的根节点。

完美 二叉树需满足：二叉树的所有父节点都有两个子节点，且所有叶子节点都在同一层。

节点的 层数 等于该节点到根节点之间的边数。

示例 1：

img

1
2
3
4
5

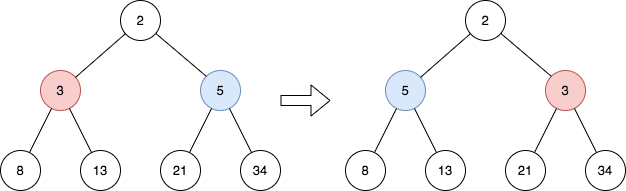
输入：root = [2,3,5,8,13,21,34]
输出：[2,5,3,8,13,21,34]
解释：
这棵树只有一个奇数层。
在第 1 层的节点分别是 3、5 ，反转后为 5、3 。

示例 2：

img

1
2
3
4

输入：root = [7,13,11]
输出：[7,11,13]
解释： 
在第 1 层的节点分别是 13、11 ，反转后为 11、13 。

示例 3：

1
2
3
4
5

输入：root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
输出：[0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
解释：奇数层由非零值组成。
在第 1 层的节点分别是 1、2 ，反转后为 2、1 。
在第 3 层的节点分别是 1、1、1、1、2、2、2、2 ，反转后为 2、2、2、2、1、1、1、1 。

提示：

  • 树中的节点数目在范围 [1, 2^14] 内
  • 0 <= Node.val <= 10^5
  • root 是一棵 完美 二叉树

解题思路

层序遍历二叉树即可

WA了一发是 取队列的首位元素加了引用，然后pop掉了，手真贱啊我

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* reverseOddLevels(TreeNode* root) {
        deque<TreeNode*> dq;
        dq.push_back(root);
        int dep = 0;
        vector<int> a;
        while(!dq.empty()){
            int sz = dq.size();
            if(dep&1) {
                 a.clear();
                
                 for(auto &node: dq){
                     a.push_back(node->val);
                 }
            }
            int j = a.size();
            // cout<<j<<endl;
            for(int i=0;i<sz;i++){
                auto u = dq.front();
                if(u->left) dq.push_back(u->left);
                if(u->right) dq.push_back(u->right);
                dq.pop_front();
                if(dep&1){
                    u->val = a[--j];
                }
            }
            dep++;
            // cout<<dep<<endl;
        }
        
        return root;
        
    }
};

偷学代码

按题意 dfs 即可。首先一遍 dfs 记录每一层从左到右的值，第二遍 dfs 替换奇数层的值即可

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    vector<vector<int>> vec;

    void dfs1(TreeNode *node, int d) {
        if (node == nullptr) return;
        if (vec.size() <= d) vec.push_back(vector<int>());
        vec[d].push_back(node->val);
        dfs1(node->left, d + 1);
        dfs1(node->right, d + 1);
    }

    void dfs2(TreeNode *node, int d) {
        if (node == nullptr) return;
        if (d & 1) node->val = vec[d].back(), vec[d].pop_back();
        dfs2(node->left, d + 1);
        dfs2(node->right, d + 1);
    }

public:
    TreeNode* reverseOddLevels(TreeNode* root) {
        dfs1(root, 0);
        dfs2(root, 0);
        return root;
    }
};

【Trie】字符串的前缀分数和

题目

给你一个长度为 n 的数组 words ，该数组由 非空 字符串组成。

定义字符串 word 的 分数 等于以 word 作为 前缀 的 words[i] 的数目。

  • 例如，如果 words = ["a", "ab", "abc", "cab"] ，那么 "ab" 的分数是 2 ，因为 "ab" 是 "ab" 和 "abc" 的一个前缀。

返回一个长度为 n 的数组 answer ，其中 answer[i] 是 words[i] 的每个非空前缀的分数 总和 。

**注意：**字符串视作它自身的一个前缀。

示例 1：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

输入：words = ["abc","ab","bc","b"]
输出：[5,4,3,2]
解释：对应每个字符串的答案如下：
- "abc" 有 3 个前缀："a"、"ab" 和 "abc" 。
- 2 个字符串的前缀为 "a" ，2 个字符串的前缀为 "ab" ，1 个字符串的前缀为 "abc" 。
总计 answer[0] = 2 + 2 + 1 = 5 。
- "ab" 有 2 个前缀："a" 和 "ab" 。
- 2 个字符串的前缀为 "a" ，2 个字符串的前缀为 "ab" 。
总计 answer[1] = 2 + 2 = 4 。
- "bc" 有 2 个前缀："b" 和 "bc" 。
- 2 个字符串的前缀为 "b" ，1 个字符串的前缀为 "bc" 。 
总计 answer[2] = 2 + 1 = 3 。
- "b" 有 1 个前缀："b"。
- 2 个字符串的前缀为 "b" 。
总计 answer[3] = 2 。

示例 2：

1
2
3
4
5

输入：words = ["abcd"]
输出：[4]
解释：
"abcd" 有 4 个前缀 "a"、"ab"、"abc" 和 "abcd"。
每个前缀的分数都是 1 ，总计 answer[0] = 1 + 1 + 1 + 1 = 4 。

提示：

  • 1 <= words.length <= 1000
  • 1 <= words[i].length <= 1000
  • words[i] 由小写英文字母组成

解题思路

前缀树模板题了属于是

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#include<iostream>
#include<cstring>
#include<deque>
#include<vector>
using namespace std;

const int MAXN = 4e6+6;
int p[MAXN][26];
int cnt[MAXN];
int root;
int tot;
void insert(string s){
    int u = root;
    for(int i=0;i<s.size();i++){
        if(!p[u][s[i]-'a']) p[u][s[i]-'a'] = ++tot;
        u = p[u][s[i]-'a'];
        cnt[u]++;
    }
}
int query(string s){
    int u = root;
    int all = 0;
    for(int i=0;i<s.size();i++){
        if(!p[u][s[i]-'a']) return -1;
        u = p[u][s[i]-'a'];
        all +=cnt[u];
    }
    return all;
}
class Solution {
public:
    vector<int> sumPrefixScores(vector<string>& words) {
        root = 0;
        tot = 0;
        memset(p,0,sizeof(p));
        memset(cnt,0,sizeof(cnt));
        for(auto &s : words) insert(s);
        vector<int> res;
        for(auto &x: words){
            res.push_back(query(x));
        }
        return res;
    }
};
Trie
Licensed under CC BY-NC-SA 4.0
© 2020 - 2024 おう てつ の blog
Built with Hugo
Theme Stack designed by Jimmy