LeetCode第314场周赛总结

【模拟】处理用时最长的那个任务的员工

题目

共有 n 位员工，每位员工都有一个从 0 到 n - 1 的唯一 id 。

给你一个二维整数数组 logs ，其中 logs[i] = [idi, leaveTimei] ：

idi 是处理第 i 个任务的员工的 id ，且
leaveTimei 是员工完成第 i 个任务的时刻。所有 leaveTimei 的值都是唯一的。

注意，第 i 个任务在第 (i - 1) 个任务结束后立即开始，且第 0 个任务从时刻 0 开始。

返回处理用时最长的那个任务的员工的 id 。如果存在两个或多个员工同时满足，则返回几人中最小的 id 。

示例 1：

1
2
3
4
5
6
7
8
输入：n = 10, logs = [[0,3],[2,5],[0,9],[1,15]]
输出：1
解释：
任务 0 于时刻 0 开始，且在时刻 3 结束，共计 3 个单位时间。
任务 1 于时刻 3 开始，且在时刻 5 结束，共计 2 个单位时间。
任务 2 于时刻 5 开始，且在时刻 9 结束，共计 4 个单位时间。
任务 3 于时刻 9 开始，且在时刻 15 结束，共计 6 个单位时间。
时间最长的任务是任务 3 ，而 id 为 1 的员工是处理此任务的员工，所以返回 1 。

示例 2：

1
2
3
4
5
6
7
8
输入：n = 26, logs = [[1,1],[3,7],[2,12],[7,17]]
输出：3
解释：
任务 0 于时刻 0 开始，且在时刻 1 结束，共计 1 个单位时间。
任务 1 于时刻 1 开始，且在时刻 7 结束，共计 6 个单位时间。
任务 2 于时刻 7 开始，且在时刻 12 结束，共计 5 个单位时间。
任务 3 于时刻 12 开始，且在时刻 17 结束，共计 5 个单位时间。
时间最长的任务是任务 1 ，而 id 为 3 的员工是处理此任务的员工，所以返回 3 。

示例 3：

1
2
3
4
5
6
输入：n = 2, logs = [[0,10],[1,20]]
输出：0
解释：
任务 0 于时刻 0 开始，且在时刻 10 结束，共计 10 个单位时间。
任务 1 于时刻 10 开始，且在时刻 20 结束，共计 10 个单位时间。
时间最长的任务是任务 0 和 1 ，处理这两个任务的员工的 id 分别是 0 和 1 ，所以返回最小的 0 。

提示：

2 <= n <= 500
1 <= logs.length <= 500
logs[i].length == 2
0 <= idi <= n - 1
1 <= leaveTimei <= 500
idi != idi + 1
leaveTimei 按严格递增顺序排列

解题思路

按题意模拟即可

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std;
class Solution {
public:
    int hardestWorker(int n, vector<vector<int>>& logs) {
        vector<int> dp(n,0);
        int m = logs.size();
        dp[logs[0][0]] = logs[0][1];
        int last = logs[0][1];
        for(int i=1;i<m;i++){
            dp[logs[i][0]] = max(dp[logs[i][0]],logs[i][1]-last);
            last = logs[i][1];
        } 
        int maxv = dp[n-1], res = n-1;
        for(int i=n-2;i>=0;i--){
            if(dp[i]>=maxv){
                maxv = dp[i];
                res = i;
            }
        }
        return res;
    }
};

【位运算/异或】找出前缀异或的原始数组

题目

给你一个长度为 n 的整数数组 pref 。找出并返回满足下述条件且长度为 n 的数组 arr ：

pref[i] = arr[0] ^ arr[1] ^ ... ^ arr[i].

注意 ^ 表示 按位异或（bitwise-xor）运算。

可以证明答案是唯一的。

示例 1：

1
2
3
4
5
6
7
8
输入：pref = [5,2,0,3,1]
输出：[5,7,2,3,2]
解释：从数组 [5,7,2,3,2] 可以得到如下结果：
- pref[0] = 5
- pref[1] = 5 ^ 7 = 2
- pref[2] = 5 ^ 7 ^ 2 = 0
- pref[3] = 5 ^ 7 ^ 2 ^ 3 = 3
- pref[4] = 5 ^ 7 ^ 2 ^ 3 ^ 2 = 1

示例 2：

1
2
3
输入：pref = [13]
输出：[13]
解释：pref[0] = arr[0] = 13

提示：

1 <= pref.length <= 10^5
0 <= pref[i] <= 10^6

解题思路

根据异或的运算性质可得，res[i] = pref[i-1] ^ pref[i]

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
public:
    vector<int> findArray(vector<int>& pref) {
        int n = pref.size();
        vector<int> res(n,0);
        res[0] = pref[0];
        for(int i=1;i<n;i++){
            res[i] = pref[i-1] ^ pref[i];
        }
        return res;
    }
};

【贪心+栈模拟】使用机器人打印字典序最小的字符串

题目

给你一个字符串 s 和一个机器人，机器人当前有一个空字符串 t 。执行以下操作之一，直到 s 和 t 都变成空字符串：

删除字符串 s 的 第一个 字符，并将该字符给机器人。机器人把这个字符添加到 t 的尾部。
删除字符串 t 的 最后一个 字符，并将该字符给机器人。机器人将该字符写到纸上。

请你返回纸上能写出的字典序最小的字符串。

示例 1：

1
2
3
4
5
6
输入：s = "zza"
输出："azz"
解释：用 p 表示写出来的字符串。
一开始，p="" ，s="zza" ，t="" 。
执行第一个操作三次，得到 p="" ，s="" ，t="zza" 。
执行第二个操作三次，得到 p="azz" ，s="" ，t="" 。

示例 2：

1
2
3
4
5
6
7
输入：s = "bac"
输出："abc"
解释：用 p 表示写出来的字符串。
执行第一个操作两次，得到 p="" ，s="c" ，t="ba" 。
执行第二个操作两次，得到 p="ab" ，s="c" ，t="" 。
执行第一个操作，得到 p="ab" ，s="" ，t="c" 。
执行第二个操作，得到 p="abc" ，s="" ，t="" 。

示例 3：

1
2
3
4
5
6
输入：s = "bdda"
输出："addb"
解释：用 p 表示写出来的字符串。
一开始，p="" ，s="bdda" ，t="" 。
执行第一个操作四次，得到 p="" ，s="" ，t="bdda" 。
执行第二个操作四次，得到 p="addb" ，s="" ，t="" 。

提示：

1 <= s.length <= 10^5
s 只包含小写英文字母。

解题思路

很可惜没写出来。看描述肯定是要用栈模拟的，再加上贪心。可惜没贪对

经典贪心：有一个初始为空的栈，给定字符的入栈顺序，求字典序最小的出栈序列。

当一个字符入栈后，我们持续检查栈顶元素 c。设还未入栈的字符中，字典序最小的字符是 m，有以下两种情况。

$c \le m$：此时弹出 c 最优。如果此时按兵不动，下一个出栈的将会是大等于 c 的字符，答案不会变优。 $c > m$：此时不弹出 c，等待后续更小的字符入栈。所有字符都入栈后，栈内的剩余字符按顺序弹出即可。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<bits/stdc++.h>
using namespace std;
class Solution {
public:
    string robotWithString(string s) {
        int n = s.size();
        vector<char> R(n+1);//R[i]: s[i..n]中最小的字符
        R[n] = 'z';
        for(int i=n-1;i>=0;i--){
            R[i] = min(R[i+1],s[i]);
        }
        stack<char> stk;
        string res;
        for(int i=0;i<n;i++){
            stk.push(s[i]);
            while(!stk.empty() && stk.top()<=R[i+1]){
                res += stk.top();
                stk.pop();
            }
        }
        return res;

    }
};

【动态规划】矩阵中和能被 K 整除的路径

题目

给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发，每一步只能往下或者往右，你想要到达终点 (m - 1, n - 1) 。

请你返回路径和能被 k 整除的路径数目，由于答案可能很大，返回答案对 10^9 + 7 取余的结果。

示例 1：

1
2
3
4
5
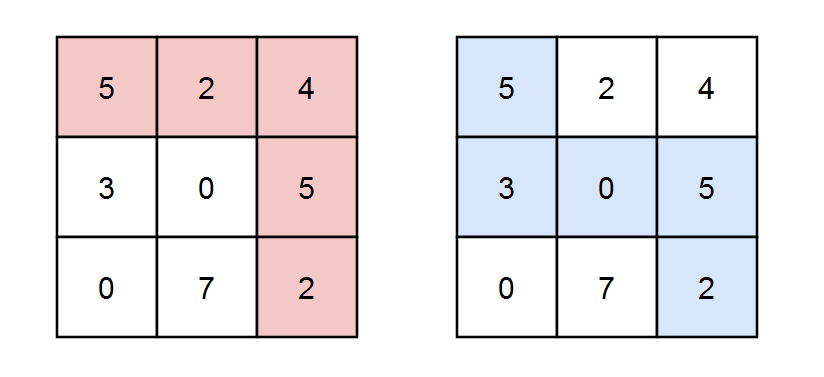
输入：grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
输出：2
解释：有两条路径满足路径上元素的和能被 k 整除。
第一条路径为上图中用红色标注的路径，和为 5 + 2 + 4 + 5 + 2 = 18 ，能被 3 整除。
第二条路径为上图中用蓝色标注的路径，和为 5 + 3 + 0 + 5 + 2 = 15 ，能被 3 整除。

示例 2：

1
2
3
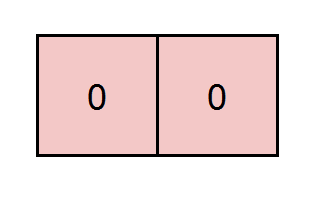
输入：grid = [[0,0]], k = 5
输出：1
解释：红色标注的路径和为 0 + 0 = 0 ，能被 5 整除。

示例 3：

1
2
3
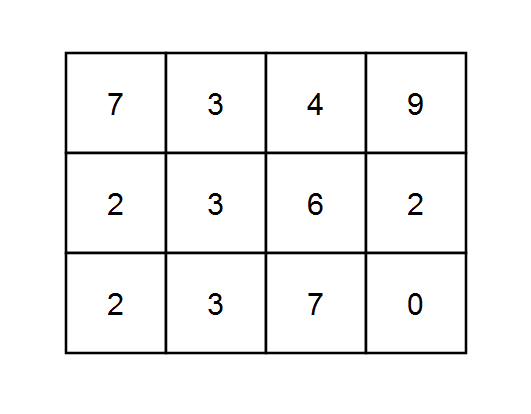
输入：grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1
输出：10
解释：每个数字都能被 1 整除，所以每一条路径的和都能被 k 整除。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 5 * 10^4
1 <= m * n <= 5 * 10^4
0 <= grid[i][j] <= 100
1 <= k <= 50

解题思路

路径类动态规划

令dp[i, j, p]表示从[0, 0]走到[i, j]过程中路径和模k等于p的路径数目

[i, j] 处状态由 [i-1, j]和[i, j-1]处转移得来

最后答案为dp[n-1, m-1, 0]

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<bits/stdc++.h>
using namespace std;
const int MOD = 1e9+7;
class Solution {
public:
    int numberOfPaths(vector<vector<int>>& grid, int k) {
        int n = grid.size(),m = grid[0].size();
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                grid[i][j] = grid[i][j]%k;
            }
        }
        long long dp[n+1][m+1][k+1];
        memset(dp,0,sizeof(dp));
        dp[0][0][grid[0][0]] = 1;
        for(int j=1;j<m;j++){
            for(int p=0;p<k;p++){
                dp[0][j][(p+grid[0][j])%k] = dp[0][j-1][p];
            }
        }
        for(int i=1;i<n;i++){
            for(int p=0;p<k;p++){
                dp[i][0][(p+grid[i][0])%k] = dp[i-1][0][p];
            }
        }
        for(int i=1;i<n;i++){
            for(int j=1;j<m;j++){
                for(int p=0;p<k;p++){
                    dp[i][j][(p+grid[i][j])%k] = (dp[i-1][j][p]+dp[i][j-1][p])%MOD;
                }
            }
        }
        return dp[n-1][m-1][0];
    }
};