LeetCode第317场周赛总结

【模拟】可被三整除的偶数的平均值

题目

给你一个由正整数组成的整数数组 nums ，返回其中可被 3 整除的所有偶数的平均值。

注意：n 个元素的平均值等于 n 个元素求和再除以 n ，结果 向下取整 到最接近的整数。

示例 1：

1
2
3
输入：nums = [1,3,6,10,12,15]
输出：9
解释：6 和 12 是可以被 3 整除的偶数。(6 + 12) / 2 = 9 。

示例 2：

1
2
3
输入：nums = [1,2,4,7,10]
输出：0
解释：不存在满足题目要求的整数，所以返回 0 。

提示：

1 <= nums.length <= 1000
1 <= nums[i] <= 1000

解题思路

按题意模拟即可

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution {
public:
    int averageValue(vector<int>& nums) {
        int n = nums.size(), m = 0, res = 0;
        for(auto &x: nums){
            if(x%2==0 && x%3==0) res+=x,m++;
        }
        if(m==0) return 0;
        return res/m;
    }
};

【哈希表】最流行的视频创作者

题目

给你两个字符串数组 creators 和 ids ，和一个整数数组 views ，所有数组的长度都是 n 。平台上第 i 个视频者是 creator[i] ，视频分配的 id 是 ids[i] ，且播放量为 views[i] 。

视频创作者的 流行度 是该创作者的所有视频的播放量的总和。请找出流行度最高创作者以及该创作者播放量最大的视频的 id 。

如果存在多个创作者流行度都最高，则需要找出所有符合条件的创作者。
如果某个创作者存在多个播放量最高的视频，则只需要找出字典序最小的 id 。

返回一个二维字符串数组 answer ，其中 answer[i] = [creatori, idi] 表示 creatori 的流行度最高且其最流行的视频 id 是 idi ，可以按任何顺序返回该结果*。*

示例 1：

1
2
3
4
5
6
7
8
9
输入：creators = ["alice","bob","alice","chris"], ids = ["one","two","three","four"], views = [5,10,5,4]
输出：[["alice","one"],["bob","two"]]
解释：
alice 的流行度是 5 + 5 = 10 。
bob 的流行度是 10 。
chris 的流行度是 4 。
alice 和 bob 是流行度最高的创作者。
bob 播放量最高的视频 id 为 "two" 。
alice 播放量最高的视频 id 是 "one" 和 "three" 。由于 "one" 的字典序比 "three" 更小，所以结果中返回的 id 是 "one" 。

示例 2：

1
2
3
4
5
输入：creators = ["alice","alice","alice"], ids = ["a","b","c"], views = [1,2,2]
输出：[["alice","b"]]
解释：
id 为 "b" 和 "c" 的视频都满足播放量最高的条件。
由于 "b" 的字典序比 "c" 更小，所以结果中返回的 id 是 "b" 。

提示：

n == creators.length == ids.length == views.length
1 <= n <= 10^5
1 <= creators[i].length, ids[i].length <= 5
creators[i] 和 ids[i] 仅由小写英文字母组成
0 <= views[i] <= 10^5

解题思路

利用两个哈希表，分别存储name->所有流行度之和， name->播放量最高且字典序最小的视频id

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#define ll long long
class Solution {
public:
    vector<vector<string>> mostPopularCreator(vector<string>& creators, vector<string>& ids, vector<int>& views) {
        int n = creators.size();
        unordered_map<string,ll> tab;//tab[name] = sum
        unordered_map<string,int> part;//part[name] = views[i]

        ll maxv = 0;
        for(int i=0;i<n;i++){
            if(tab.count(creators[i])){
                tab[creators[i]] += views[i];
                int &u = part[creators[i]];
                if(views[i]>views[u] || (views[i]==views[u] && ids[i]<ids[u])){
                   u = i;
                }
            }else{
                tab[creators[i]] = views[i];
                part[creators[i]] = i;
            }
            maxv = max(maxv, tab[creators[i]]);
        }

        vector<vector<string>> res;
        for(auto it=part.begin();it!=part.end();it++){
            if(tab[it->first] == maxv){
                res.push_back({it->first, ids[it->second]});
            }
        }

        return res;

    }
};

【数学&模拟进位】美丽整数的最小增量

题目

给你两个正整数 n 和 target 。

如果某个整数每一位上的数字相加小于或等于 target ，则认为这个整数是一个 美丽整数 。

找出并返回满足 n + x 是 美丽整数 的最小非负整数 x 。生成的输入保证总可以使 n 变成一个美丽整数。

示例 1：

1
2
3
输入：n = 16, target = 6
输出：4
解释：最初，n 是 16 ，且其每一位数字的和是 1 + 6 = 7 。在加 4 之后，n 变为 20 且每一位数字的和变成 2 + 0 = 2 。可以证明无法加上一个小于 4 的非负整数使 n 变成一个美丽整数。

示例 2：

1
2
3
输入：n = 467, target = 6
输出：33
解释：最初，n 是 467 ，且其每一位数字的和是 4 + 6 + 7 = 17 。在加 33 之后，n 变为 500 且每一位数字的和变成 5 + 0 + 0 = 5 。可以证明无法加上一个小于 33 的非负整数使 n 变成一个美丽整数。

示例 3：

1
2
3
输入：n = 1, target = 1
输出：0
解释：最初，n 是 1 ，且其每一位数字的和是 1 ，已经小于等于 target 。

提示：

1 <= n <= 10^12
1 <= target <= 150
生成的输入保证总可以使 n 变成一个美丽整数。

解题思路

首先考虑怎样才能使数位和减小？

只可能加上x使得原数产生进位才有可能，否则不进位的话，数位和是不可能减小的

所以从个位开始模拟进位即可

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#define ll long long
class Solution {
public:
    long long makeIntegerBeautiful(long long n, int target) {
        vector<int> stk;
        int ori = 0;
        ll m = n;
        while(m){
            stk.push_back(m%10);
            ori += m%10;
            m = m/10;
        }
        if(ori<=target) return 0;//如果一开始数位和就小于等于target
        ll tail = 1, res = 0;
        reverse(stk.begin(),stk.end());
        while(!stk.empty()){//低位到高位
           
            int u = stk.back();//当前位
            //必须产生进位才可能能使得数位和减小
            int need = 10 - u;//当前位进位所需要的加数 
            stk.pop_back();
            ori -= u;//进位的话 当前位就变成0了
            int carry = 1;//向前进位
            for(int i=stk.size()-1;i>=0;i--){//模拟进位过程
                stk[i] += carry;
                ori += 1;//进位后数位和加1
                if(stk[i]==10){//可以继续进位
                    carry = 1;
                    ori -= 10;
                    stk[i]=0;
                }else{
                    carry = 0;
                    break;
                }
            }
            if(carry) {//
                ori += 1;
                stk.insert(stk.begin(),1);
            }

            res += 1ll * need * tail;
            tail *= 10;
            
            if(ori <= target) break;
        }

        return res;

    }
};

【DFS序+时间戳】移除子树后的二叉树高度

题目

给你一棵 二叉树 的根节点 root ，树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。

你必须在树上执行 m 个独立的查询，其中第 i 个查询你需要执行以下操作：

从树中移除以 queries[i] 的值作为根节点的子树。题目所用测试用例保证 queries[i] 不等于根节点的值。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是执行第 i 个查询后树的高度。

注意：

查询之间是独立的，所以在每个查询执行后，树会回到其初始状态。
树的高度是从根到树中某个节点的 最长简单路径中的边数 。

示例 1：

1
2
3
4
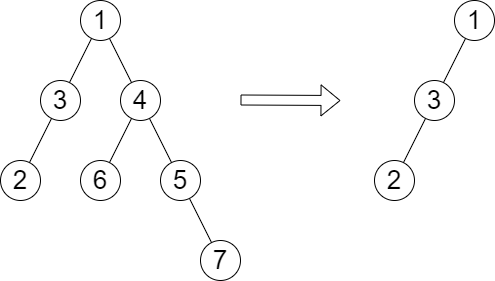
输入：root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
输出：[2]
解释：上图展示了从树中移除以 4 为根节点的子树。
树的高度是 2（路径为 1 -> 3 -> 2）。

示例 2：

1
2
3
4
5
6
7
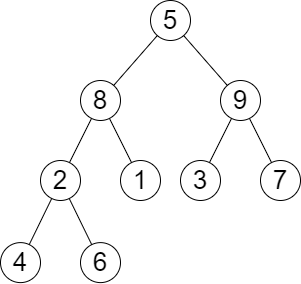
输入：root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
输出：[3,2,3,2]
解释：执行下述查询：
- 移除以 3 为根节点的子树。树的高度变为 3（路径为 5 -> 8 -> 2 -> 4）。
- 移除以 2 为根节点的子树。树的高度变为 2（路径为 5 -> 8 -> 1）。
- 移除以 4 为根节点的子树。树的高度变为 3（路径为 5 -> 8 -> 2 -> 6）。
- 移除以 8 为根节点的子树。树的高度变为 2（路径为 5 -> 9 -> 3）。

提示：

树中节点的数目是 n
2 <= n <= 10^5
1 <= Node.val <= n
树中的所有值 互不相同
m == queries.length
1 <= m <= min(n, 10^4)
1 <= queries[i] <= n
queries[i] != root.val

解题思路

子树里的所有点是 DFS 序里的一个连续区间。因此本题可以被转化为如下问题：

给定一个序列，每次删除一个连续区间，求序列里剩下的数的最大值。

显然删除一个连续区间后，序列会剩下一个前缀以及一个后缀。我们预处理前缀 max 和后缀 max，就能 $\mathcal{O}(1)$ 回答每个询问。复杂度 $\mathcal{O}(n + q)$。

即转化为DFS序后，利用时间戳找到在DFS序中的位置，子树在DFS序中是连续的一段值。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
const int MAXN =  1e5+5;
class Solution {
public:
    vector<int> treeQueries(TreeNode* root, vector<int>& queries) {
        int time = 0;
        vector<int> dfsorder(MAXN,0);
        vector<int> in(MAXN,0), out(MAXN,0), d(MAXN,0);
        //dfsorder[i]  dfs序列 第i个表示 时间i dfs序列上节点的值
        //in[i] 时间戳 值为i的节点 的入时间
        //out[i] 时间戳 值为i的节点 的出时间
        function<void(TreeNode*,int)> dfs=[&](TreeNode* root, int dep)->void{
            in[root->val] = ++time;
            dfsorder[time] = root->val;
            d[root->val] = dep;
            if(root->left){
                dfs(root->left, dep+1);
            }
            if(root->right){
                dfs(root->right, dep+1);
            }
            out[root->val] = time;
        };
        dfs(root,0);

        vector<int> f(MAXN, 0),g(MAXN, 0);
        int n = time;
        for(int i=1;i<=n;i++){
            f[i] = max(f[i-1], d[dfsorder[i]]);
        }
        for(int i=n;i>=1;i--){
            g[i] = max(g[i+1], d[dfsorder[i]]);
        }

        vector<int> res;
        for(auto &u: queries){
            int l = in[u], r = out[u];
            res.push_back(max(f[l-1], g[r+1]));
        }

        return res;
    }
};