Featured image of post LeetCode第318场周赛总结
leetcode contest

LeetCode第318场周赛总结

---/5670

【模拟】对数组执行操作

题目

给你一个下标从 0 开始的数组 nums ，数组大小为 n ，且由 非负 整数组成。

你需要对数组执行 n - 1 步操作，其中第 i 步操作（从 0 开始计数）要求对 nums 中第 i 个元素执行下述指令：

  • 如果 nums[i] == nums[i + 1] ，则 nums[i] 的值变成原来的 2 倍，nums[i + 1] 的值变成 0 。否则，跳过这步操作。

在执行完 全部 操作后，将所有 0 移动 到数组的 末尾 。

  • 例如，数组 [1,0,2,0,0,1] 将所有 0 移动到末尾后变为 [1,2,1,0,0,0] 。

返回结果数组。

注意 操作应当 依次有序 执行，而不是一次性全部执行。

示例 1：

1
2
3
4
5
6
7
8
9

输入：nums = [1,2,2,1,1,0]
输出：[1,4,2,0,0,0]
解释：执行以下操作：
- i = 0: nums[0] 和 nums[1] 不相等，跳过这步操作。
- i = 1: nums[1] 和 nums[2] 相等，nums[1] 的值变成原来的 2 倍，nums[2] 的值变成 0 。数组变成 [1,4,0,1,1,0] 。
- i = 2: nums[2] 和 nums[3] 不相等，所以跳过这步操作。
- i = 3: nums[3] 和 nums[4] 相等，nums[3] 的值变成原来的 2 倍，nums[4] 的值变成 0 。数组变成 [1,4,0,2,0,0] 。
- i = 4: nums[4] 和 nums[5] 相等，nums[4] 的值变成原来的 2 倍，nums[5] 的值变成 0 。数组变成 [1,4,0,2,0,0] 。
执行完所有操作后，将 0 全部移动到数组末尾，得到结果数组 [1,4,2,0,0,0] 。

示例 2：

1
2
3

输入：nums = [0,1]
输出：[1,0]
解释：无法执行任何操作，只需要将 0 移动到末尾。

提示：

  • 2 <= nums.length <= 2000
  • 0 <= nums[i] <= 1000

解题思路

按题意模拟即可

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    vector<int> applyOperations(vector<int>& nums) {
        int n = nums.size();
        vector<int> res;
        for(int i=0;i<n-1;i++){
            if(nums[i]==nums[i+1]) nums[i]*=2,nums[i+1]=0;
        }
        for(int i=0;i<n;i++){
            if(nums[i]!=0) res.push_back(nums[i]);
        }
        for(int i=0;i<n;i++){
            if(nums[i]==0) res.push_back(nums[i]);
        }
        return res;
    }
};

【枚举】长度为 K 子数组中的最大和

题目

给你一个整数数组 nums 和一个整数 k 。请你从 nums 中满足下述条件的全部子数组中找出最大子数组和：

  • 子数组的长度是 k，且
  • 子数组中的所有元素 各不相同 。

返回满足题面要求的最大子数组和。如果不存在子数组满足这些条件，返回 0 。

子数组 是数组中一段连续非空的元素序列。

示例 1：

1
2
3
4
5
6
7
8
9

输入：nums = [1,5,4,2,9,9,9], k = 3
输出：15
解释：nums 中长度为 3 的子数组是：
- [1,5,4] 满足全部条件，和为 10 。
- [5,4,2] 满足全部条件，和为 11 。
- [4,2,9] 满足全部条件，和为 15 。
- [2,9,9] 不满足全部条件，因为元素 9 出现重复。
- [9,9,9] 不满足全部条件，因为元素 9 出现重复。
因为 15 是满足全部条件的所有子数组中的最大子数组和，所以返回 15 。

示例 2：

1
2
3
4
5

输入：nums = [4,4,4], k = 3
输出：0
解释：nums 中长度为 3 的子数组是：
- [4,4,4] 不满足全部条件，因为元素 4 出现重复。
因为不存在满足全部条件的子数组，所以返回 0 。

提示：

  • 1 <= k <= nums.length <= 10^5
  • 1 <= nums[i] <= 10^5

解题思路

枚举长度为k的子数组即可

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

#define ll long long
class Solution {
public:
    long long maximumSubarraySum(vector<int>& nums, int k) {
        int n = nums.size();
        ll res = 0,cur=0;
        int l=0,r=0;
        unordered_map<int,int> tab;
        for(int i=0;i<k;i++){
            tab[nums[i]]++;
            cur += nums[i];
        }
        if(tab.size() == k) res = max(res, cur);
        // cout<<res<<endl;
        for(int i=k;i<n;i++){
            if(--tab[nums[i-k]]==0) tab.erase(nums[i-k]);
            tab[nums[i]]++;
            cur += nums[i];
            cur -= nums[i-k];
            if(tab.size() == k) res = max(res, cur);
        }
        return res;
    }
};

【模拟】雇佣 K 位工人的总代价

题目

给你一个下标从 0 开始的整数数组 costs ，其中 costs[i] 是雇佣第 i 位工人的代价。

同时给你两个整数 k 和 candidates 。我们想根据以下规则恰好雇佣 k 位工人：

  • 总共进行 k 轮雇佣，且每一轮恰好雇佣一位工人。

  • 在每一轮雇佣中，从最前面

    1

    candidates

    和最后面

    1

    candidates

    人中选出代价最小的一位工人，如果有多位代价相同且最小的工人，选择下标更小的一位工人。

    • 比方说，costs = [3,2,7,7,1,2] 且 candidates = 2 ，第一轮雇佣中，我们选择第 4 位工人，因为他的代价最小 [3,2,7,7,1,2] 。
    • 第二轮雇佣，我们选择第 1 位工人，因为他们的代价与第 4 位工人一样都是最小代价，而且下标更小，[3,2,7,7,2] 。注意每一轮雇佣后，剩余工人的下标可能会发生变化。

  • 如果剩余员工数目不足 candidates 人，那么下一轮雇佣他们中代价最小的一人，如果有多位代价相同且最小的工人，选择下标更小的一位工人。

  • 一位工人只能被选择一次。

返回雇佣恰好 k 位工人的总代价。

示例 1：

1
2
3
4
5
6
7

输入：costs = [17,12,10,2,7,2,11,20,8], k = 3, candidates = 4
输出：11
解释：我们总共雇佣 3 位工人。总代价一开始为 0 。
- 第一轮雇佣，我们从 [17,12,10,2,7,2,11,20,8] 中选择。最小代价是 2 ，有两位工人，我们选择下标更小的一位工人，即第 3 位工人。总代价是 0 + 2 = 2 。
- 第二轮雇佣，我们从 [17,12,10,7,2,11,20,8] 中选择。最小代价是 2 ，下标为 4 ，总代价是 2 + 2 = 4 。
- 第三轮雇佣，我们从 [17,12,10,7,11,20,8] 中选择，最小代价是 7 ，下标为 3 ，总代价是 4 + 7 = 11 。注意下标为 3 的工人同时在最前面和最后面 4 位工人中。
总雇佣代价是 11 。

示例 2：

1
2
3
4
5
6
7

输入：costs = [1,2,4,1], k = 3, candidates = 3
输出：4
解释：我们总共雇佣 3 位工人。总代价一开始为 0 。
- 第一轮雇佣，我们从 [1,2,4,1] 中选择。最小代价为 1 ，有两位工人，我们选择下标更小的一位工人，即第 0 位工人，总代价是 0 + 1 = 1 。注意，下标为 1 和 2 的工人同时在最前面和最后面 3 位工人中。
- 第二轮雇佣，我们从 [2,4,1] 中选择。最小代价为 1 ，下标为 2 ，总代价是 1 + 1 = 2 。
- 第三轮雇佣，少于 3 位工人，我们从剩余工人 [2,4] 中选择。最小代价是 2 ，下标为 0 。总代价为 2 + 2 = 4 。
总雇佣代价是 4 。

提示：

  • 1 <= costs.length <= 10^5
  • 1 <= costs[i] <= 10^5
  • 1 <= k, candidates <= costs.length

解题思路

利用堆（或set）等数据结构维护工人信息即可

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

#include<bits/stdc++.h>
using namespace std;
#define ll long long
struct node{
    int val,pos,dir;
    node(int v,int p,int d){
        val= v,pos = p, dir=d;
    }
    friend bool operator < (const node &a, const node &b){
        if(a.val!=b.val) return a.val<b.val;
        return a.pos<b.pos;
    }
};
class Solution {
public:
    
    long long totalCost(vector<int>& costs, int k, int candidates) {
        int n = costs.size();
        int l = 0,r = n-1;
        set<node> tab;
        while(l<n && l<candidates) {
            tab.insert(node(costs[l],l,0));
            l++;
        }
        while(r>=l && n-r-1 < candidates){
            tab.insert(node(costs[r],r,1));
            r--;
        }
        ll res = 0;
        // for(auto &x: tab){
        //     cout<<x.val<<' '<<x.pos<<' '<<x.dir<<endl;
        // }
        for(int i=0;i<k;i++){
            node top = *tab.begin();
            tab.erase(tab.begin());
            // cout<<top.val<<' '<<top.pos<<' '<<top.dir<<endl;
            res += top.val;
            if(r<l) continue;
            if(top.dir==0){
                tab.insert(node(costs[l],l,0));
                l++;
            }else{
                tab.insert(node(costs[r],r,1));
                r--;
            }
        }
        return res;
    }
};

【dp/记忆化搜索】最小移动总距离

题目

X 轴上有一些机器人和工厂。给你一个整数数组 robot ，其中 robot[i] 是第 i 个机器人的位置。再给你一个二维整数数组 factory ，其中 factory[j] = [positionj, limitj] ，表示第 j 个工厂的位置在 positionj ，且第 j 个工厂最多可以修理 limitj 个机器人。

每个机器人所在的位置 互不相同 。每个工厂所在的位置也 互不相同 。注意一个机器人可能一开始跟一个工厂在 相同的位置 。

所有机器人一开始都是坏的，他们会沿着设定的方向一直移动。设定的方向要么是 X 轴的正方向，要么是 X 轴的负方向。当一个机器人经过一个没达到上限的工厂时，这个工厂会维修这个机器人，且机器人停止移动。

任何时刻，你都可以设置 部分 机器人的移动方向。你的目标是最小化所有机器人总的移动距离。

请你返回所有机器人移动的最小总距离。测试数据保证所有机器人都可以被维修。

注意：

  • 所有机器人移动速度相同。
  • 如果两个机器人移动方向相同，它们永远不会碰撞。
  • 如果两个机器人迎面相遇，它们也不会碰撞，它们彼此之间会擦肩而过。
  • 如果一个机器人经过了一个已经达到上限的工厂，机器人会当作工厂不存在，继续移动。
  • 机器人从位置 x 到位置 y 的移动距离为 |y - x| 。

示例 1：

img

1
2
3
4
5
6
7
8
9

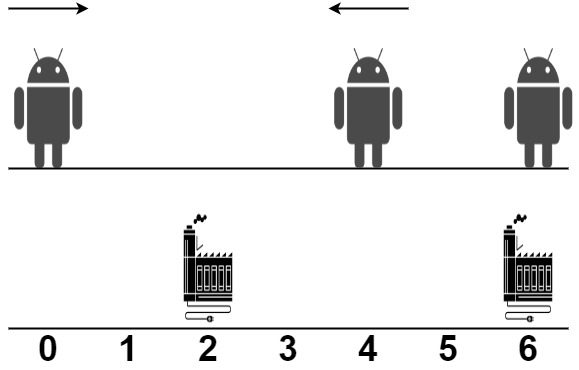
输入：robot = [0,4,6], factory = [[2,2],[6,2]]
输出：4
解释：如上图所示：
- 第一个机器人从位置 0 沿着正方向移动，在第一个工厂处维修。
- 第二个机器人从位置 4 沿着负方向移动，在第一个工厂处维修。
- 第三个机器人在位置 6 被第二个工厂维修，它不需要移动。
第一个工厂的维修上限是 2 ，它维修了 2 个机器人。
第二个工厂的维修上限是 2 ，它维修了 1 个机器人。
总移动距离是 |2 - 0| + |2 - 4| + |6 - 6| = 4 。没有办法得到比 4 更少的总移动距离。

示例 2：

img

1
2
3
4
5
6
7
8

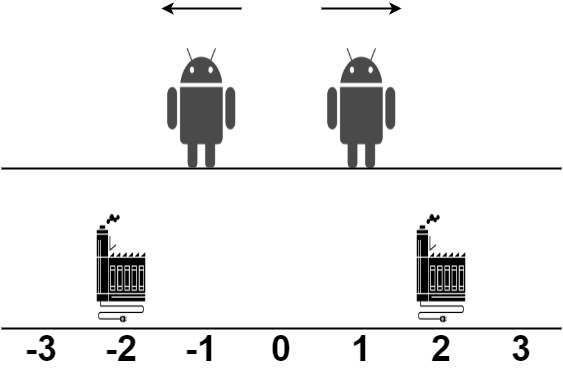
输入：robot = [1,-1], factory = [[-2,1],[2,1]]
输出：2
解释：如上图所示：
- 第一个机器人从位置 1 沿着正方向移动，在第二个工厂处维修。
- 第二个机器人在位置 -1 沿着负方向移动，在第一个工厂处维修。
第一个工厂的维修上限是 1 ，它维修了 1 个机器人。
第二个工厂的维修上限是 1 ，它维修了 1 个机器人。
总移动距离是 |2 - 1| + |(-2) - (-1)| = 2 。没有办法得到比 2 更少的总移动距离。

提示：

  • 1 <= robot.length, factory.length <= 100
  • factory[j].length == 2
  • -10^9 <= robot[i], positionj <= 10^9
  • 0 <= limitj <= robot.length
  • 测试数据保证所有机器人都可以被维修。

解题思路

注意一个重要结论，一个工厂肯定是负责一段连续的机器人，不会出现交叉的情况，可以反证（交换邻项）

利用dp[i][j]表示 工厂[i..n-1]修理机器人[j..m-1]所需的最小移动总距离

枚举最后一个工厂修理机器人的个数进行状态转移

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#define ll long long
const ll INF = LONG_MAX;
class Solution {
public:
    long long minimumTotalDistance(vector<int>& robot, vector<vector<int>>& factory) {
        int n = factory.size(), m = robot.size();
        sort(robot.begin(), robot.end());
        sort(factory.begin(), factory.end(),[&](vector<int>& a, vector<int>& b){
            return a[0]<b[0];
        });
        //
        vector<vector<ll>> dp(n+1,vector<ll>(m+1,INF));
        //dp[i][j] 表示 工厂[i..n-1]修理机器人[j..m-1]所需的最小移动总距离
        function<ll(int,int)> dfs=[&](int i,int j)->ll{
            if(dp[i][j]!=INF) return dp[i][j];
            if(j==m) return 0;
            if(i==n-1){
                if(m-j>factory[i][1]) return INF/2;
                ll res = 0;
                for(int k=j;k<m;k++) res += abs(robot[k]-factory[i][0]);
                return res;
            }
            ll sum = dfs(i+1,j);//第i个工厂不修 任何一个机器人
            int k=1;//枚举第i个工厂修k个机器人
            ll cur = 0;
            while(k<=factory[i][1] && j+k-1<m){
                cur += abs(robot[j+k-1] - factory[i][0]);
                sum = min(sum, cur + dfs(i+1, j+k));
                k++;
            }
            return dp[i][j] = sum;
        };
        return dfs(0,0);

    }
};
© 2020 - 2024 おう てつ の blog
Built with Hugo
Theme Stack designed by Jimmy