没打
【模拟】温度转换
题目
给你一个四舍五入到两位小数的非负浮点数 celsius 来表示温度,以 摄氏度(Celsius)为单位。
你需要将摄氏度转换为 开氏度(Kelvin)和 华氏度(Fahrenheit),并以数组 ans = [kelvin, fahrenheit] 的形式返回结果。
返回数组 ans 。与实际答案误差不超过 10-5 的会视为正确答案**。**
注意:
开氏度 = 摄氏度 + 273.15华氏度 = 摄氏度 * 1.80 + 32.00
示例 1 :
1
2
3
| 输入:celsius = 36.50
输出:[309.65000,97.70000]
解释:36.50 摄氏度:转换为开氏度是 309.65 ,转换为华氏度是 97.70 。
|
示例 2 :
1
2
3
| 输入:celsius = 122.11
输出:[395.26000,251.79800]
解释:122.11 摄氏度:转换为开氏度是 395.26 ,转换为华氏度是 251.798 。
|
提示:
解题思路
简单模拟即可
代码
1
2
3
4
5
6
| class Solution {
public:
vector<double> convertTemperature(double celsius) {
return {celsius+273.15, celsius*1.80+32.00};
}
};
|
【枚举】最小公倍数为 K 的子数组数目
题目
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 nums 的 子数组 中满足 元素最小公倍数为 k的子数组数目。
子数组 是数组中一个连续非空的元素序列。
数组的最小公倍数 是可被所有数组元素整除的最小正整数。
示例 1 :
1
2
3
4
5
6
7
| 输入:nums = [3,6,2,7,1], k = 6
输出:4
解释:以 6 为最小公倍数的子数组是:
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
|
示例 2 :
1
2
3
| 输入:nums = [3], k = 2
输出:0
解释:不存在以 2 为最小公倍数的子数组。
|
提示:
1 <= nums.length <= 10001 <= nums[i], k <= 1000
解题思路
枚举
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public:
int lcm(int a, int b){
return a*b/__gcd(a,b);
}
int subarrayLCM(vector<int>& nums, int k) {
int n = nums.size(), res = 0;
for(int i=0;i<n;i++){
if(nums[i] == k) res++;
int mv = nums[i];
for(int j=i+1;j<n;j++){
mv = lcm(mv, nums[j]);
if(mv==k) res++;
if(mv>k) break;
}
}
return res;
}
};
|
【模拟】逐层排序二叉树所需的最少操作数目
题目
给你一个 值互不相同 的二叉树的根节点 root 。
在一步操作中,你可以选择 同一层 上任意两个节点,交换这两个节点的值。
返回每一层按 严格递增顺序 排序所需的最少操作数目。
节点的 层数 是该节点和根节点之间的路径的边数。
示例 1 :
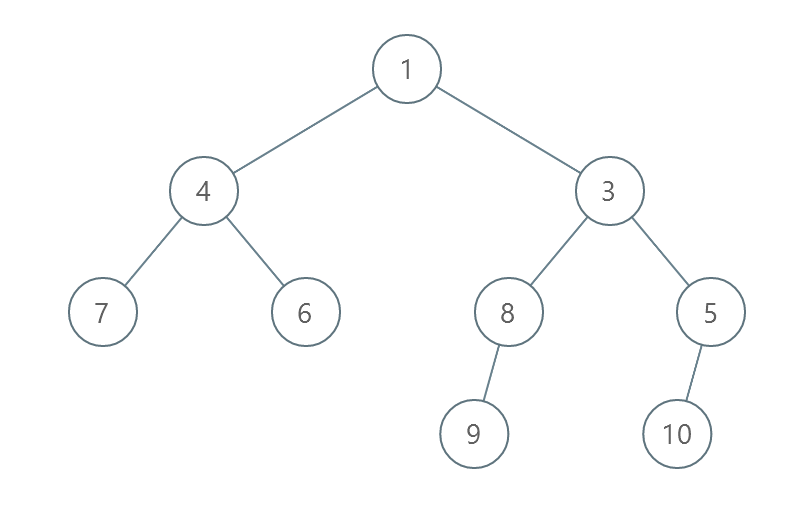
1
2
3
4
5
6
7
8
| 输入:root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出:3
解释:
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作,所以返回 3 。
可以证明 3 是需要的最少操作数目。
|
示例 2 :
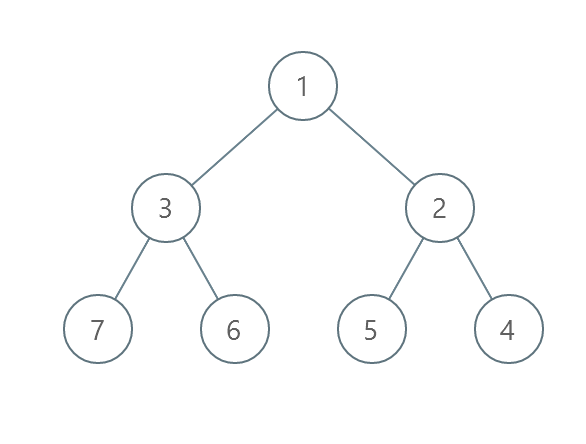
1
2
3
4
5
6
7
8
| 输入:root = [1,3,2,7,6,5,4]
输出:3
解释:
- 交换 3 和 2 。第 2 层变为 [2,3] 。
- 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。
- 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
共计用了 3 步操作,所以返回 3 。
可以证明 3 是需要的最少操作数目。
|
示例 3 :
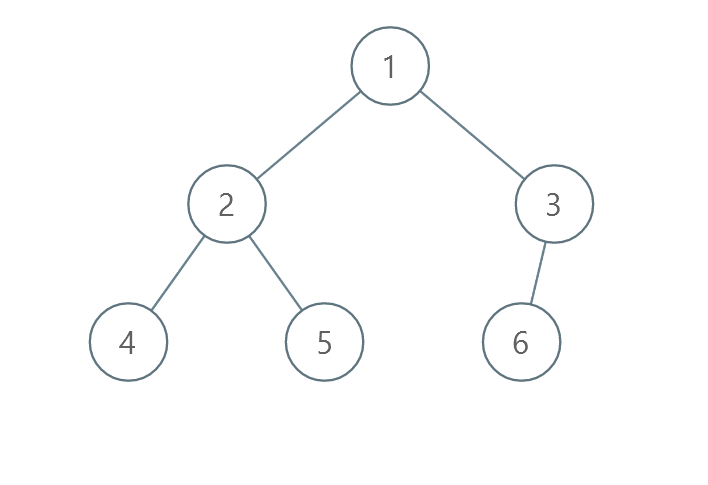
1
2
3
| 输入:root = [1,2,3,4,5,6]
输出:0
解释:每一层已经按递增顺序排序,所以返回 0 。
|
提示:
- 树中节点的数目在范围
[1, 10^5] 。 1 <= Node.val <= 10^5- 树中的所有值 互不相同 。
解题思路
按层序遍历,取出每一层的数
转化为子问题:给一个序列,序列两两元素可以任意交换,求最少的交换次数使得序列有序
一般有两种做法(详见 https://www.geeksforgeeks.org/minimum-number-swaps-required-sort-array/ )
1、从1到n枚举下标i。设当前序列第i个位置的数为ai,目标序列的第i个位置的数为bi。若ai!=bi,则不断将ai交换到目标位置,直到ai=bi。交换次数就是答案。
2、求整个序列中置换环的数量,答案就是序列长度减去置换环的数量
作者:TsReaper
链接:https://leetcode.cn/circle/discuss/rYjnBt/view/y0qjkB/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minimumOperations(TreeNode* root) {
queue<TreeNode*> que;
que.push(root);
int res = 0;
while(!que.empty()){
int sz = que.size();
vector<int> row;
for(int i=0;i<sz;i++){
TreeNode* top = que.front();
row.push_back(top->val);
if(top->left) que.push(top->left);
if(top->right) que.push(top->right);
que.pop();
}
vector<int> tar(row.begin(),row.end());
sort(tar.begin(),tar.end());
int n = tar.size();
unordered_map<int,int> tab;
for(int i=0;i<n;i++){
tab[tar[i]] = i;
}
for(int i=0;i<n;i++){
while(row[i]!=tar[i]){
swap(row[i], row[tab[row[i]]]);
res ++;
}
}
}
return res;
}
};
|
【中心拓展算法+DP】不重叠回文子字符串的最大数目
题目
给你一个字符串 s 和一个 正 整数 k 。
从字符串 s 中选出一组满足下述条件且 不重叠 的子字符串:
- 每个子字符串的长度 至少 为
k 。 - 每个子字符串是一个 回文串 。
返回最优方案中能选择的子字符串的 最大 数目。
子字符串 是字符串中一个连续的字符序列。
示例 1 :
1
2
3
4
| 输入:s = "abaccdbbd", k = 3
输出:2
解释:可以选择 s = "abaccdbbd" 中斜体加粗的子字符串。"aba" 和 "dbbd" 都是回文,且长度至少为 k = 3 。
可以证明,无法选出两个以上的有效子字符串。
|
示例 2 :
1
2
3
| 输入:s = "adbcda", k = 2
输出:0
解释:字符串中不存在长度至少为 2 的回文子字符串。
|
提示:
1 <= k <= s.length <= 2000s 仅由小写英文字母组成
解题思路
由中心拓展算法,枚举中心位点
令dp[i] 表示s[0..i-1]的合法不重叠回文子字符串最大数目
考虑s[r]在不在回文子串内
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public:
int maxPalindromes(string s, int k) {
int n = s.size();
vector<int> dp(n+1, 0);
//dp[i] : s[0..i-1]的合法不重叠回文子字符串最大数目
for(int i=0;i<2*n-1;i++){//2n-1组中心点
int l = i/2, r = l+i%2;//
dp[r+1] = max(dp[r+1], dp[r]);//如果s[r]不在回文子串内
while(l>=0 && r<n && s[l]==s[r]){
if(r-l+1>=k) {
dp[r+1] = max(dp[r+1], 1+dp[l]);
break;//可break
}
l--,r++;
}
}
return dp[n];
}
};
|



