
【模拟】数组中不等三元组的数目
题目
给你一个下标从 0 开始的正整数数组 nums 。请你找出并统计满足下述条件的三元组 (i, j, k) 的数目:
0 <= i < j < k < nums.length- nums[i]、nums[j]和nums[k]两两不同。
- 换句话说:
nums[i] != nums[j]、nums[i] != nums[k] 且 nums[j] != nums[k] 。
返回满足上述条件三元组的数目*。*
示例 1:
1
2
3
4
5
6
7
8
| 输入:nums = [4,4,2,4,3]
输出:3
解释:下面列出的三元组均满足题目条件:
- (0, 2, 4) 因为 4 != 2 != 3
- (1, 2, 4) 因为 4 != 2 != 3
- (2, 3, 4) 因为 2 != 4 != 3
共计 3 个三元组,返回 3 。
注意 (2, 0, 4) 不是有效的三元组,因为 2 > 0 。
|
示例 2:
1
2
3
| 输入:nums = [1,1,1,1,1]
输出:0
解释:不存在满足条件的三元组,所以返回 0 。
|
提示:
3 <= nums.length <= 1001 <= nums[i] <= 1000
解题思路
简单模拟即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
class Solution {
public:
int unequalTriplets(vector<int>& nums) {
int n = nums.size();
int res = 0;
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
for(int k=j+1;k<n;k++){
if(nums[i]!=nums[j] && nums[j]!=nums[k] && nums[i]!=nums[k]) res++;
}
}
}
return res;
}
};
|
【二分】二叉搜索树最近节点查询
题目
给你一个 二叉搜索树 的根节点 root ,和一个由正整数组成、长度为 n 的数组 queries 。
请你找出一个长度为 n 的 二维 答案数组 answer ,其中 answer[i] = [mini, maxi] :
mini 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值,则使用 -1 代替。maxi 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值,则使用 -1 代替。
返回数组 answer 。
示例 1 :
1
2
3
4
5
6
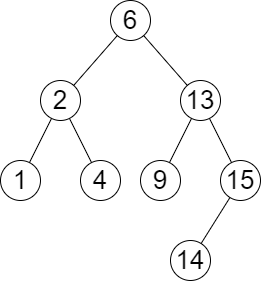
| 输入:root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
输出:[[2,2],[4,6],[15,-1]]
解释:按下面的描述找出并返回查询的答案:
- 树中小于等于 2 的最大值是 2 ,且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。
- 树中小于等于 5 的最大值是 4 ,且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。
- 树中小于等于 16 的最大值是 15 ,且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。
|
示例 2 :
1
2
3
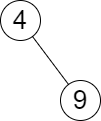
| 输入:root = [4,null,9], queries = [3]
输出:[[-1,4]]
解释:树中不存在小于等于 3 的最大值,且大于等于 3 的最小值是 4 。所以查询的答案是 [-1,4] 。
|
提示:
- 树中节点的数目在范围
[2, 10^5] 内 1 <= Node.val <= 10^6n == queries.length1 <= n <= 10^51 <= queries[i] <= 10^6
解题思路
二叉搜索树进行中序遍历得到有序数组,然后进行二分查找即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> a;
void dfs(TreeNode* root){
if(root->left) dfs(root->left);
a.push_back(root->val);
if(root->right) dfs(root->right);
}
vector<vector<int>> closestNodes(TreeNode* root, vector<int>& queries) {
dfs(root);
int n = a.size();
// for(int i=0;i<n;i++) cout<<a[i]<<' ';
vector<vector<int>> res;
for(auto &u: queries){
int idx = lower_bound(a.begin(),a.end(),u)-a.begin();
int l=-1,r=-1;
if(idx!=n) r = a[idx];
if(idx!=0) l = a[idx-1];
if(idx!=n && a[idx]==u) l=u;
res.push_back({l,r});
}
return res;
}
};
|
【树型DP+贪心】到达首都的最少油耗
题目
给你一棵 n 个节点的树(一个无向、连通、无环图),每个节点表示一个城市,编号从 0 到 n - 1 ,且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ,其中 roads[i] = [ai, bi] ,表示城市 ai 和 bi 之间有一条 双向路 。
每个城市里有一个代表,他们都要去首都参加一个会议。
每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目。
城市里的代表可以选择乘坐所在城市的车,或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。
请你返回到达首都最少需要多少升汽油。
示例 1:
1
2
3
4
5
6
7
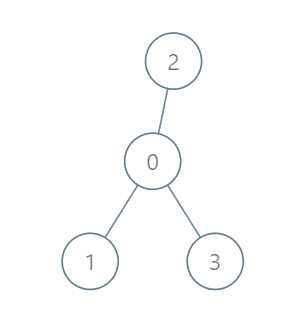
| 输入:roads = [[0,1],[0,2],[0,3]], seats = 5
输出:3
解释:
- 代表 1 直接到达首都,消耗 1 升汽油。
- 代表 2 直接到达首都,消耗 1 升汽油。
- 代表 3 直接到达首都,消耗 1 升汽油。
最少消耗 3 升汽油。
|
示例 2:
1
2
3
4
5
6
7
8
9
10
11
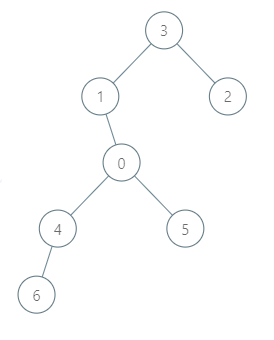
| 输入:roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
输出:7
解释:
- 代表 2 到达城市 3 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到达城市 1 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到达首都,消耗 1 升汽油。
- 代表 1 直接到达首都,消耗 1 升汽油。
- 代表 5 直接到达首都,消耗 1 升汽油。
- 代表 6 到达城市 4 ,消耗 1 升汽油。
- 代表 4 和代表 6 一起到达首都,消耗 1 升汽油。
最少消耗 7 升汽油。
|
示例 3:

1
2
3
| 输入:roads = [], seats = 1
输出:0
解释:没有代表需要从别的城市到达首都。
|
提示:
1 <= n <= 10^5roads.length == n - 1roads[i].length == 20 <= ai, bi < nai != biroads 表示一棵合法的树。1 <= seats <= 10^5
解题思路
注意到一个关键结论:所有车只往根节点移动。此时的油耗会最少
赛时统计了每个子树的大小sz,每个子树的人cnt,以及每个子树所需的油耗dp
其实可以同时统计
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
class Solution {
public:
long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
int n = roads.size() + 1;
vector<int> G[n+1];
for(auto &x: roads){
G[x[0]].push_back(x[1]);
G[x[1]].push_back(x[0]);
}
vector<int> sz(n+1,0);
function<int(int, int)> dfs = [&](int u, int fa)->int{
sz[u] = 1;
for(auto &v: G[u]){
if(v==fa) continue;
dfs(v, u);
sz[u] += sz[v];
}
return sz[u];
};
dfs(0,-1);
// for(int i=0;i<n;i++){
// cout<<sz[i]<<endl;
// }
vector<ll> dp(n, 0);
vector<int> cnt(n,0);
function<void(int,int)> f=[&](int u, int fa)->void{
if(sz[u] == 1){
dp[u] = 0;
cnt[u] = 1;
return;
}
ll cur = 0;
int sum = 1;
for(auto &v: G[u]){
if(v == fa) continue;
f(v, u);
cur += dp[v];
sum += cnt[v];
if(cnt[v]%seats==0) cur+=cnt[v]/seats;
else cur+=cnt[v]/seats+1;
}
dp[u] = cur;
cnt[u] = sum;
};
f(0,-1);
// for(int i=0;i<n;i++){
// cout<<i<<' '<<sz[i]<<' '<<cnt[i]<<' '<<dp[i]<<endl;
// }
return dp[0];
}
};
|
偷学代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public:
long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
int n = roads.size() + 1;
// 建图
vector<int> e[n];
for (auto &road : roads) {
e[road[0]].push_back(road[1]);
e[road[1]].push_back(road[0]);
}
long long ans = 0;
// DFS 统计子树大小,同时统计答案
function<int(int, int)> dfs = [&](int sn, int fa) {
int ret = 1;
// 如果是叶子结点的话 子树大小为1
for (int fn : e[sn]) if (fn != fa) {
// 计算 sn -> fn 这条边的贡献
int t = dfs(fn, sn);
ans += (t + seats - 1) / seats;
// 更新子树大小
ret += t;
}
return ret;
};
dfs(0, -1);
return ans;
}
};
|
作者:TsReaper
链接:https://leetcode.cn/circle/discuss/bb9NEI/view/c5Ok3w/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
【DP】完美分割的方案数
题目
给你一个字符串 s ,每个字符是数字 '1' 到 '9' ,再给你两个整数 k 和 minLength 。
如果对 s 的分割满足以下条件,那么我们认为它是一个 完美 分割:
s 被分成 k 段互不相交的子字符串。- 每个子字符串长度都 至少 为
minLength 。 - 每个子字符串的第一个字符都是一个 质数 数字,最后一个字符都是一个 非质数 数字。质数数字为
'2' ,'3' ,'5' 和 '7' ,剩下的都是非质数数字。
请你返回 s 的 完美 分割数目。由于答案可能很大,请返回答案对 109 + 7 取余 后的结果。
一个 子字符串 是字符串中一段连续字符串序列。
示例 1:
1
2
3
4
5
6
| 输入:s = "23542185131", k = 3, minLength = 2
输出:3
解释:存在 3 种完美分割方案:
"2354 | 218 | 5131"
"2354 | 21851 | 31"
"2354218 | 51 | 31"
|
示例 2:
1
2
3
| 输入:s = "23542185131", k = 3, minLength = 3
输出:1
解释:存在一种完美分割方案:"2354 | 218 | 5131" 。
|
示例 3:
1
2
3
| 输入:s = "3312958", k = 3, minLength = 1
输出:1
解释:存在一种完美分割方案:"331 | 29 | 58" 。
|
提示:
1 <= k, minLength <= s.length <= 1000s 每个字符都为数字 '1' 到 '9' 之一。
解题思路
令dp[i][j]表示 s[0..i-1]分成j段的方案总数
考虑s[i-1]成为第j段的结尾时的情况,还需要枚举第j段的开头。
s[i-1]需要为非质数,s[t-1]需要为质数
$$
dp[i][j] = \sum_t^{i-minLength}dp[t][j-1]
$$
故可在 $O(n*n*k)$ 时间内考虑所有情况
考虑优化
注意到上式t是递增,可由前缀和维护,利用g[i][j]维护相应前缀和即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| const int MOD = 1e9+7;
#define ll long long
class Solution {
public:
bool prime(char x){
if(x=='2'||x=='3'||x=='5'||x=='7') return true;
return false;
}
int beautifulPartitions(string s, int k, int minLength) {
int n = s.size();
if(k*minLength>n || !prime(s[0]) || prime(s[n-1])) return 0;
vector<vector<ll>> dp(n+1, vector<ll>(k+1, 0));
//dp[i][j] : s[0..i-1] 分成j 段的方案数
dp[0][0] = 1;//空字符串
vector<vector<ll>> g(n+1, vector<ll>(k+1, 0));
//g[i][j] : \sum_t^{i} dp[t][j-1]
g[0][0] = 1;
for(int i=1;i<=n;i++) g[i][0] = g[i-1][0] + 0;
for(int j=1;j<=k;j++){
for(int i=1;i<=n;i++){//以s[i-1]为第j段的结尾
// if(j*minLength>i) continue;
// for(int t=0;t<i;t++){//枚举这一段的开始位置
// if(!prime(s[i-1]) && prime(s[t]) && i-t>=minLength){
// dp[i][j] = (dp[i][j] + dp[t][j-1])%MOD;
// }
// }
//s[i-1]为第j段结尾时,s[i-1]需为非质数
//还需要考虑第j段的开始,但是也可以直接考虑第j+1段的开始,即s[i]
//s[i]需为质数 或者 字符串结束
if(i>=minLength && !prime(s[i-1]) && (i==n || prime(s[i]))){
dp[i][j] = g[i-minLength][j-1];
}
}
g[0][j] = dp[0][j];
for(int i=1;i<=n;i++){
g[i][j] = (g[i-1][j] + dp[i][j])%MOD;
}
}
return dp[n][k];
}
};
|






