Featured image of post LeetCode第361场周赛总结
leetcode contest

LeetCode第361场周赛总结

451/4170

image-20230906213201110

时隔9个月，再度打周赛，人少了好多呀

# 【模拟】统计对称整数的数目

# 题目

给你两个正整数 low 和 high 。

对于一个由 2 * n 位数字组成的整数 x ，如果其前 n 位数字之和与后 n 位数字之和相等，则认为这个数字是一个对称整数。

返回在 [low, high] 范围内的 对称整数的数目 。

示例 1：

1
2
3

输入：low = 1, high = 100
输出：9
解释：在 1 到 100 范围内共有 9 个对称整数：11、22、33、44、55、66、77、88 和 99 。

示例 2：

1
2
3

输入：low = 1200, high = 1230
输出：4
解释：在 1200 到 1230 范围内共有 4 个对称整数：1203、1212、1221 和 1230 。

提示：

  • 1 <= low <= high <= 10^4

# 解题思路

按题意模拟

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

#include<bits/stdc++.h>
using namespace std;
class Solution {
public:
    bool isok(int num){
        string s = to_string(num);
        int n = s.size();
        if(n%2==1) return false;
        int front = 0;
        for(int i=0;i<n/2;i++){
            front += s[i]-'0';
        }
        int back = 0;
        for(int i=n/2;i<n;i++){
            back += s[i]-'0';
        }
        return front==back;
    }
    int countSymmetricIntegers(int low, int high) {
        int res = 0;
        for(int i=low;i<=high;i++) if(isok(i)) res++;
        return res;
    }
};

# 【枚举】生成特殊数字的最少操作

# 题目

给你一个下标从 0 开始的字符串 num ，表示一个非负整数。

在一次操作中，您可以选择 num 的任意一位数字并将其删除。请注意，如果你删除 num 中的所有数字，则 num 变为 0。

返回最少需要多少次操作可以使 num 变成特殊数字。

如果整数 x 能被 25 整除，则该整数 x 被认为是特殊数字。

示例 1：

1
2
3
4

输入：num = "2245047"
输出：2
解释：删除数字 num[5] 和 num[6] ，得到数字 "22450" ，可以被 25 整除。
可以证明要使数字变成特殊数字，最少需要删除 2 位数字。

示例 2：

1
2
3
4

输入：num = "2908305"
输出：3
解释：删除 num[3]、num[4] 和 num[6] ，得到数字 "2900" ，可以被 25 整除。
可以证明要使数字变成特殊数字，最少需要删除 3 位数字。

示例 3：

1
2
3
4

输入：num = "10"
输出：1
解释：删除 num[0] ，得到数字 "0" ，可以被 25 整除。
可以证明要使数字变成特殊数字，最少需要删除 1 位数字。

提示

  • 1 <= num.length <= 100
  • num 仅由数字 '0' 到 '9' 组成
  • num 不含任何前导零

# 解题思路

如果一个数能被25整除，那么这个数的末尾一定是00，25，50，或75

还有一种可能是删成0

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

#include<bits/stdc++.h>
using namespace std;
class Solution {
public:
    //25 00 50 75
    int case4(string num, string tar){
        stack<char> stk;
        for(auto &x: tar) stk.push(x);
        int res = 0, n = num.size();
        for(int i=n-1;i>=0;i--){
            if(!stk.empty()){
                if(stk.top()==num[i]){//不用删
                    res ++;
                    stk.pop();
                }
            }else res++;
        }
        if(stk.empty()) return n-res;
        return n;
    }
    int case0(string num){
        int n = num.size();
        int res = 0;
        for(int i=n-1;i>=0;i--){
            if(num[i]=='0'){
                return n-1;
            }
        }
        return n;
    }
    int minimumOperations(string num) {
        if(num=="0") return 0;
        int res = num.size();
        // cout<<case4(num, "0")<<endl;
        res = min(res, case4(num, "25"));
        res = min(res, case4(num, "00"));
        res = min(res, case4(num, "75"));
        res = min(res, case4(num, "50"));
        res = min(res, case0(num));
        return res;

    }
};

# 【哈希表+前缀和】统计趣味子数组的数目

# 题目

给你一个下标从 0 开始的整数数组 nums ，以及整数 modulo 和整数 k 。

请你找出并统计数组中 趣味子数组 的数目。

如果 子数组 nums[l..r] 满足下述条件，则称其为 趣味子数组 ：

  • 在范围 [l, r] 内，设 cnt 为满足 nums[i] % modulo == k 的索引 i 的数量。并且 cnt % modulo == k 。

以整数形式表示并返回趣味子数组的数目。

**注意：**子数组是数组中的一个连续非空的元素序列。

示例 1：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

输入：nums = [3,2,4], modulo = 2, k = 1
输出：3
解释：在这个示例中，趣味子数组分别是： 
子数组 nums[0..0] ，也就是 [3] 。 
- 在范围 [0, 0] 内，只存在 1 个下标 i = 0 满足 nums[i] % modulo == k 。
- 因此 cnt = 1 ，且 cnt % modulo == k 。
子数组 nums[0..1] ，也就是 [3,2] 。
- 在范围 [0, 1] 内，只存在 1 个下标 i = 0 满足 nums[i] % modulo == k 。
- 因此 cnt = 1 ，且 cnt % modulo == k 。
子数组 nums[0..2] ，也就是 [3,2,4] 。
- 在范围 [0, 2] 内，只存在 1 个下标 i = 0 满足 nums[i] % modulo == k 。
- 因此 cnt = 1 ，且 cnt % modulo == k 。
可以证明不存在其他趣味子数组。因此，答案为 3 。

示例 2：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

输入：nums = [3,1,9,6], modulo = 3, k = 0
输出：2
解释：在这个示例中，趣味子数组分别是： 
子数组 nums[0..3] ，也就是 [3,1,9,6] 。
- 在范围 [0, 3] 内，只存在 3 个下标 i = 0, 2, 3 满足 nums[i] % modulo == k 。
- 因此 cnt = 3 ，且 cnt % modulo == k 。
子数组 nums[1..1] ，也就是 [1] 。
- 在范围 [1, 1] 内，不存在下标满足 nums[i] % modulo == k 。
- 因此 cnt = 0 ，且 cnt % modulo == k 。
可以证明不存在其他趣味子数组，因此答案为 2 。

提示：

  • 1 <= nums.length <= 10^5
  • 1 <= nums[i] <= 10^9
  • 1 <= modulo <= 10^9
  • 0 <= k < modulo

# 解题思路

将满足$nums[i]\ mod\ modulo =k $的$nums[i]$视作1，不满足则视作0；

计算前缀和数组cnt，对于区间[l, r]，有 $$ (s[r]-s[l-1])\ mod\ modulo = k $$ 等价于 $$ (s[r]-k)\ mod\ modulo = s[l-1]\ mod\ modulo $$ 从左到右枚举，利用哈希表维护之前的信息。

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

#include<bits/stdc++.h>
using namespace std;
#define ll long long
class Solution {
public:
    long long countInterestingSubarrays(vector<int>& nums, int modulo, int k) {
        int n = nums.size();
        vector<ll> cnt(n+1,0);
        unordered_map<ll,ll> tab;//tab[i]=j 前缀数量为i的有j个
        tab[0] = 1;
        ll res = 0;
        for(int i=1;i<=n;i++){
            cnt[i] = cnt[i-1] + (nums[i-1]%modulo==k);
            //  (cnt[i]-x)%modulo==k
            ll tar = (cnt[i]%modulo-k+modulo)%modulo;
            res += tab[tar];
            tab[cnt[i]%modulo] ++;
        }
        return res;
    }
};

# 【倍增求LCA+枚举】边权重均等查询

# 题目

现有一棵由 n 个节点组成的无向树，节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。

另给你一个长度为 m 的二维整数数组 queries ，其中 queries[i] = [ai, bi] 。对于每条查询，请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中，你可以选择树上的任意一条边，并将其权重更改为任意值。

注意：

  • 查询之间 相互独立 的，这意味着每条新的查询时，树都会回到 初始状态 。
  • 从 ai 到 bi的路径是一个由 不同 节点组成的序列，从节点 ai 开始，到节点 bi 结束，且序列中相邻的两个节点在树中共享一条边。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是第 i 条查询的答案。

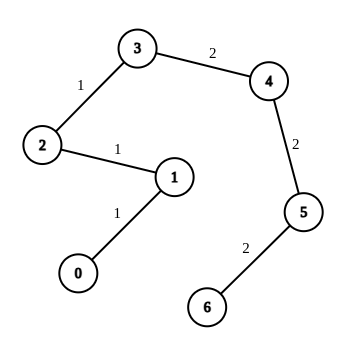
示例 1：

img

1
2
3
4
5
6
7

输入：n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
输出：[0,0,1,3]
解释：第 1 条查询，从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此，答案为 0 。
第 2 条查询，从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 0 。
第 3 条查询，将边 [2,3] 的权重变更为 2 。在这次操作之后，从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 1 。
第 4 条查询，将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后，从节点 0 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 3 。
对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

示例 2：

img

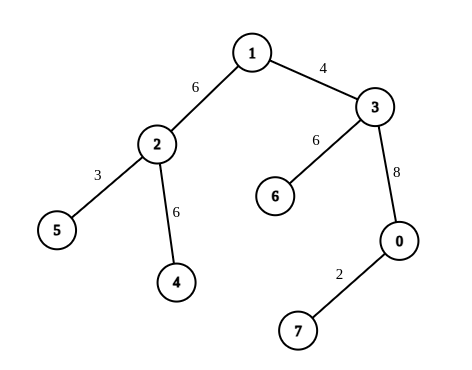
1
2
3
4
5
6
7

输入：n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]
输出：[1,2,2,3]
解释：第 1 条查询，将边 [1,3] 的权重变更为 6 。在这次操作之后，从节点 4 到节点 6 的路径中的所有边的权重都是 6 。因此，答案为 1 。
第 2 条查询，将边 [0,3]、[3,1] 的权重变更为 6 。在这次操作之后，从节点 0 到节点 4 的路径中的所有边的权重都是 6 。因此，答案为 2 。
第 3 条查询，将边 [1,3]、[5,2] 的权重变更为 6 。在这次操作之后，从节点 6 到节点 5 的路径中的所有边的权重都是 6 。因此，答案为 2 。
第 4 条查询，将边 [0,7]、[0,3]、[1,3] 的权重变更为 6 。在这次操作之后，从节点 7 到节点 4 的路径中的所有边的权重都是 6 。因此，答案为 3 。
对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

提示：

  • 1 <= n <= 10^4
  • edges.length == n - 1
  • edges[i].length == 3
  • 0 <= ui, vi < n
  • 1 <= wi <= 26
  • 生成的输入满足 edges 表示一棵有效的树
  • 1 <= queries.length == m <= 2 * 104
  • queries[i].length == 2
  • 0 <= ai, bi < n

# 解题思路

倍增求LCA

利用倍增算法求LCA，通过LCA算出两节点距离。注意到边权范围为[1,26]，在倍增过程中枚举记录每个边权的数量，求出两节点间每个边权最多的数目，操作使得所有边权都变成这个。

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

#define P pair<int,int>
class Solution {
public:
    vector<int> minOperationsQueries(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {
        vector<vector<P>> G(n);
        vector<int> d(n,-1);
        vector<vector<int>> pa(n,vector<int>(32,-1));
        vector<vector<array<int,27>>> cnt(n,vector<array<int,27>>(32));
       //cnt[i][j][k]: 节点i到 其第2^j的祖先节点路径中 k 的个数
       //pa[i][j]: 节点i的第2^j个祖先节点
        for(auto &edge: edges){
            G[edge[0]].emplace_back(edge[1], edge[2]);
            G[edge[1]].emplace_back(edge[0], edge[2]);
        }
        function<void(int,int)> dfs = [&](int u, int fa)->void{
            for(auto &vw: G[u]){
                int v = vw.first;
                int w = vw.second;
                if(v==fa) continue;
                cnt[v][0][w] = 1;
                d[v] = d[u] + 1;
                pa[v][0] = u;
                dfs(v, u);
            }
        };
        d[0] = 0;
        pa[0][0] = -1;
        dfs(0, -1);
        // for(int i=0;i<n;i++) cout<<d[i]<<' ';cout<<endl;
        
        int m = 32 - __builtin_clz(n);
        // cout<<"m: "<<m<<endl;

        for(int j=1;j<m;j++){//层级在外循环
            for(int i=0;i<n;i++){
                if(pa[i][j-1]!=-1){
                    pa[i][j] = pa[pa[i][j-1]][j-1];
                    for(int k=1;k<=26;k++){
                        cnt[i][j][k] = cnt[i][j-1][k]+cnt[pa[i][j-1]][j-1][k];
                    }
                }
                    
            }
        }
      
        vector<int> res;
        for(auto &query: queries){
            int p = query[0], q = query[1];
            int path = d[p]+d[q];
            if(d[p]<d[q]) swap(p,q);
            vector<int> cw(27,0);
            for(int j=m-1;j>=0;j--){
                if(pa[p][j]==-1) continue;
                if(d[pa[p][j]]>=d[q]){
                    for(int k=1;k<=26;k++){
                        cw[k] += cnt[p][j][k];
                    }
                    p = pa[p][j];
                }
            }
            if(p!=q){
                for(int j=m-1;j>=0;j--){
                    if(pa[p][j]==-1 || pa[q][j]==-1) continue;
                    if(pa[p][j]!=pa[q][j]){
                        for(int k=1;k<=26;k++){
                            cw[k] += cnt[p][j][k];
                            cw[k] += cnt[q][j][k];
                        }
                        p = pa[p][j];
                        q = pa[q][j];
                    }
                }
                for(int k=1;k<=26;k++){
                    cw[k] += cnt[p][0][k];
                    cw[k] += cnt[q][0][k];
                }
                p = pa[p][0];
                q = pa[q][0];
            }
            int lca = p;
            path -= 2*d[lca];
            int maxv = *max_element(cw.begin(),cw.end());
            // cout<<lca<<' '<<path<<' '<<maxv<<endl;
            res.push_back(path-maxv);
        }

        return res;
    }
};
LCA
Licensed under CC BY-NC-SA 4.0
Last updated on Sep 06, 2023 00:00 UTC
© 2020 - 2024 おう てつ の blog
Built with Hugo
Theme Stack designed by Jimmy