LeetCode第76场双周赛总结

【模拟】找到最接近0的数字

题目

给你一个长度为 n 的整数数组 nums ，请你返回 nums 中最接近 0 的数字。如果有多个答案，请你返回它们中的 最大值 。

示例 1：

1
2
3
4
5
6
7
8
9
输入：nums = [-4,-2,1,4,8]
输出：1
解释：
-4 到 0 的距离为 |-4| = 4 。
-2 到 0 的距离为 |-2| = 2 。
1 到 0 的距离为 |1| = 1 。
4 到 0 的距离为 |4| = 4 。
8 到 0 的距离为 |8| = 8 。
所以，数组中距离 0 最近的数字为 1 。

示例 2：

1
2
3
输入：nums = [2,-1,1]
输出：1
解释：1 和 -1 都是距离 0 最近的数字，所以返回较大值 1 。

提示：

1 <= n <= 1000
-105 <= nums[i] <= 10^5

解题思路

找绝对值最小的，若相同则选正数

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution {
public:
    int findClosestNumber(vector<int>& nums) {
        int res = nums[0];
        for(auto x: nums){
            if(abs(x) < abs(res)) res = x;
            else if(abs(x) == abs(res)) res = max(res, x);
        }
        return res;
    }
};

【枚举】买钢笔和铅笔的方案数

题目

给你一个整数 total ，表示你拥有的总钱数。同时给你两个整数 cost1 和 cost2 ，分别表示一支钢笔和一支铅笔的价格。你可以花费你部分或者全部的钱，去买任意数目的两种笔。

请你返回购买钢笔和铅笔的 不同方案数目 。

示例 1：

1
2
3
4
5
6
7
输入：total = 20, cost1 = 10, cost2 = 5
输出：9
解释：一支钢笔的价格为 10 ，一支铅笔的价格为 5 。
- 如果你买 0 支钢笔，那么你可以买 0 ，1 ，2 ，3 或者 4 支铅笔。
- 如果你买 1 支钢笔，那么你可以买 0 ，1 或者 2 支铅笔。
- 如果你买 2 支钢笔，那么你没法买任何铅笔。
所以买钢笔和铅笔的总方案数为 5 + 3 + 1 = 9 种。

示例 2：

1
2
3
输入：total = 5, cost1 = 10, cost2 = 10
输出：1
解释：钢笔和铅笔的价格都为 10 ，都比拥有的钱数多，所以你没法购买任何文具。所以只有 1 种方案：买 0 支钢笔和 0 支铅笔。

提示：

1 <= total, cost1, cost2 <= 10^6

解题思路

先算出最多买钢笔的数量max1，那么钢笔可买范围为[0,max1]

然后再算出铅笔可买数量范围

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Solution {
public:
    long long waysToBuyPensPencils(int total, int cost1, int cost2) {
        long long max1 = total/cost1;
        long long res = 0;
        for(int i=0;i<=max1;i++){//钢笔
            long long rest = (long long)total - i*cost1;
            long long max2 = rest/cost2;
            
            res += (max2-0+1);
        }
        return res;
    }
};

【模拟】设计一个 ATM 机器

题目

一个 ATM 机器，存有 5 种面值的钞票：20 ，50 ，100 ，200 和 500 美元。初始时，ATM 机是空的。用户可以用它存或者取任意数目的钱。

取款时，机器会优先取较大数额的钱。

比方说，你想取 $300 ，并且机器里有 2 张 $50 的钞票，1 张 $100 的钞票和1 张 $200 的钞票，那么机器会取出 $100 和 $200 的钞票。
但是，如果你想取 $600 ，机器里有 3 张 $200 的钞票和1 张 $500 的钞票，那么取款请求会被拒绝，因为机器会先取出 $500 的钞票，然后无法取出剩余的 $100 。注意，因为有 $500 钞票的存在，机器不能取 $200 的钞票。

请你实现 ATM 类：

ATM() 初始化 ATM 对象。
void deposit(int[] banknotesCount) 分别存入 $20 ，$50，$100，$200 和 $500 钞票的数目。
int[] withdraw(int amount) 返回一个长度为 5 的数组，分别表示 $20 ，$50，$100 ，$200 和 $500 钞票的数目，并且更新 ATM 机里取款后钞票的剩余数量。如果无法取出指定数额的钱，请返回 [-1] （这种情况下不取出任何钞票）。

示例 1：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
输入：
["ATM", "deposit", "withdraw", "deposit", "withdraw", "withdraw"]
[[], [[0,0,1,2,1]], [600], [[0,1,0,1,1]], [600], [550]]
输出：
[null, null, [0,0,1,0,1], null, [-1], [0,1,0,0,1]]

解释：
ATM atm = new ATM();
atm.deposit([0,0,1,2,1]); // 存入 1 张 $100 ，2 张 $200 和 1 张 $500 的钞票。
atm.withdraw(600);        // 返回 [0,0,1,0,1] 。机器返回 1 张 $100 和 1 张 $500 的钞票。机器里剩余钞票的数量为 [0,0,0,2,0] 。
atm.deposit([0,1,0,1,1]); // 存入 1 张 $50 ，1 张 $200 和 1 张 $500 的钞票。
                          // 机器中剩余钞票数量为 [0,1,0,3,1] 。
atm.withdraw(600);        // 返回 [-1] 。机器会尝试取出 $500 的钞票，然后无法得到剩余的 $100 ，所以取款请求会被拒绝。
                          // 由于请求被拒绝，机器中钞票的数量不会发生改变。
atm.withdraw(550);        // 返回 [0,1,0,0,1] ，机器会返回 1 张 $50 的钞票和 1 张 $500 的钞票。

提示：

banknotesCount.length == 5
0 <= banknotesCount[i] <= 10^9
1 <= amount <= 10^9
总共最多有 5000 次 withdraw 和 deposit 的调用。
函数 withdraw 和 deposit 至少各有一次调用。

解题思路

模拟即可

但这题的数据范围很搞啊

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class ATM {
private:
    vector<long long> money;//每种钞票的数量
public:
    ATM() {
        money.assign(5,0);//20 50 100 200 500
    }
    void deposit(vector<int> banknotesCount) {
        for(int i=0;i<5;i++){
            money[i] += banknotesCount[i];
            // cout<<money[i]<<' ';
        }
        
    }
    
    vector<int> withdraw(int amount) {
    
        vector<long long> res(5,0);
        int val[5] = {20,50,100,200,500};
        for(int i=4;i>=0;i--){
            long long need = amount/val[i];
            need = min(need, money[i]);
            amount -= need*val[i];
            res[i] = need;
        }
        if(amount) 
            return {-1}; 
        else {
            for(int i=0;i<5;i++) money[i]-=res[i];
            return vector<int>(res.begin(),res.end());
        }
        
    }
};

/**
 * Your ATM object will be instantiated and called as such:
 * ATM* obj = new ATM();
 * obj->deposit(banknotesCount);
 * vector<int> param_2 = obj->withdraw(amount);
 */

【枚举】节点序列的最大得分

题目

给你一个 n 个节点的 无向图 ，节点编号为 0 到 n - 1 。

给你一个下标从 0 开始的整数数组 scores ，其中 scores[i] 是第 i 个节点的分数。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] ，表示节点 ai 和 bi 之间有一条无向边。

一个合法的节点序列如果满足以下条件，我们称它是 合法的 ：

序列中每相邻节点之间有边相连。
序列中没有节点出现超过一次。

节点序列的分数定义为序列中节点分数之和。

请你返回一个长度为 4 的合法节点序列的最大分数。如果不存在这样的序列，请你返回 -1 。

示例 1：

1
2
3
4
5
6
7
输入：scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
输出：24
解释：上图为输入的图，节点序列为 [0,1,2,3] 。
节点序列的分数为 5 + 2 + 9 + 8 = 24 。
观察可知，没有其他节点序列得分和超过 24 。
注意节点序列 [3,1,2,0] 和 [1,0,2,3] 也是合法的，且分数为 24 。
序列 [0,3,2,4] 不是合法的，因为没有边连接节点 0 和 3 。

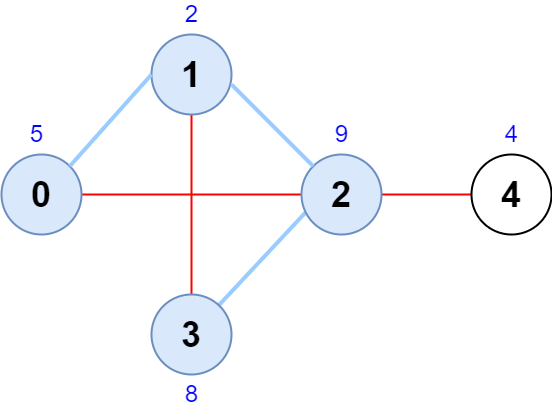
示例 2：

1
2
3
4
输入：scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]]
输出：-1
解释：上图为输入的图。
没有长度为 4 的合法序列，所以我们返回 -1 。

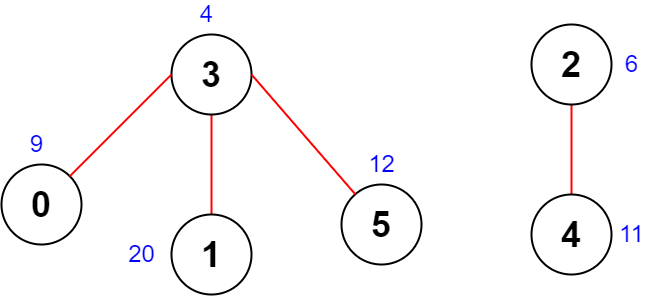
提示：

n == scores.length
4 <= n <= 5 * 10^4
1 <= scores[i] <= 10^8
0 <= edges.length <= 5 * 10^4
edges[i].length == 2
0 <= ai, bi <= n - 1
ai != bi
不会有重边。

解题思路

思路很有意思

要找一个长度为4的链，可以先枚举中间的2个节点u和v（链中间的那条边）。为了让链的点权值之和最大，那么剩下的两个点应该选择与u相邻的，排除v以外权值最大的点a , 以及与v相邻的，排除u以外权值最大的点b。

注意特殊情况：点a和点b不能是同一个点，所以需要找出与u相邻的最大的3个点。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#define P pair<int,int>
class Solution {
public:
    vector<vector<P>> G;
    int maximumScore(vector<int>& scores, vector<vector<int>>& edges) {
        int n = scores.size();
        G.resize(n);
        for(auto x: edges){
            int u = x[0],v=x[1];
            G[u].push_back(P(v,scores[v]));
            G[v].push_back(P(u,scores[u]));
        }

        for(int i=0;i<n;i++){
            sort(G[i].begin(),G[i].end(),[&](P a, P b){
                return a.second>b.second;
            });
        }//邻接表，按权值从大到小排列

        int res = -1;

        for(auto x: edges){
            int u=x[0],v=x[1];//枚举中间的两个点
            for(int i=0;i<3 && i<G[u].size();i++){//和点u连接的最大权值的3个点
                int a = G[u][i].first;
                for(int j=0;j<3 && j<G[v].size();j++){//和点v连接的最大权值的3个点
                    int b = G[v][j].first;
                    if(a!=b && a!=v && b!=u){//互不相等时更新答案
                        res = max(res, scores[u]+scores[v]+scores[a]+scores[b]);
                    }
                }
            } 
        }
        return res;
    }
};