
【模拟】统计是给定字符串前缀的字符串数目
题目
给你一个字符串数组 words 和一个字符串 s ,其中 words[i] 和 s 只包含 小写英文字母 。
请你返回 words 中是字符串 s 前缀 的 字符串数目 。
一个字符串的 前缀 是出现在字符串开头的子字符串。子字符串 是一个字符串中的连续一段字符序列。
示例 1:
1
2
3
4
5
6
| 输入:words = ["a","b","c","ab","bc","abc"], s = "abc"
输出:3
解释:
words 中是 s = "abc" 前缀的字符串为:
"a" ,"ab" 和 "abc" 。
所以 words 中是字符串 s 前缀的字符串数目为 3 。
|
示例 2:
1
2
3
4
5
| 输入:words = ["a","a"], s = "aa"
输出:2
解释:
两个字符串都是 s 的前缀。
注意,相同的字符串可能在 words 中出现多次,它们应该被计数多次。
|
提示:
1 <= words.length <= 10001 <= words[i].length, s.length <= 10words[i] 和 s 只 包含小写英文字母。
解题思路
简单模拟即可
比赛过程中还是脑袋转的慢
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
bool isok(string s, string t){
if(s.size()>t.size()) return false;
for(int i=0;i<s.size();i++){
if(s[i]!=t[i]) return false;
}
return true;
}
int countPrefixes(vector<string>& words, string s) {
int res = 0;
for(auto &str:words){
if(isok(str,s)) res++;
}
return res;
}
};
|
偷学代码
1
2
3
4
5
6
7
8
| class Solution {
public:
int countPrefixes(vector<string>& words, string s) {
int ret=0;
for(auto i:words)ret+=(s.substr(0,i.size())==i);
return ret;
}
};
|
【枚举、前缀和】最小平均差
题目
给你一个下标从 0 开始长度为 n 的整数数组 nums 。
下标 i 处的 平均差 指的是 nums 中 前 i + 1 个元素平均值和 后 n - i - 1 个元素平均值的 绝对差 。两个平均值都需要 向下取整 到最近的整数。
请你返回产生 最小平均差 的下标。如果有多个下标最小平均差相等,请你返回 最小 的一个下标。
注意:
- 两个数的 绝对差 是两者差的绝对值。
n 个元素的平均值是 n 个元素之 和 除以(整数除法) n 。0 个元素的平均值视为 0 。
示例 1:
1
2
3
4
5
6
7
8
9
10
| 输入:nums = [2,5,3,9,5,3]
输出:3
解释:
- 下标 0 处的平均差为:|2 / 1 - (5 + 3 + 9 + 5 + 3) / 5| = |2 / 1 - 25 / 5| = |2 - 5| = 3 。
- 下标 1 处的平均差为:|(2 + 5) / 2 - (3 + 9 + 5 + 3) / 4| = |7 / 2 - 20 / 4| = |3 - 5| = 2 。
- 下标 2 处的平均差为:|(2 + 5 + 3) / 3 - (9 + 5 + 3) / 3| = |10 / 3 - 17 / 3| = |3 - 5| = 2 。
- 下标 3 处的平均差为:|(2 + 5 + 3 + 9) / 4 - (5 + 3) / 2| = |19 / 4 - 8 / 2| = |4 - 4| = 0 。
- 下标 4 处的平均差为:|(2 + 5 + 3 + 9 + 5) / 5 - 3 / 1| = |24 / 5 - 3 / 1| = |4 - 3| = 1 。
- 下标 5 处的平均差为:|(2 + 5 + 3 + 9 + 5 + 3) / 6 - 0| = |27 / 6 - 0| = |4 - 0| = 4 。
下标 3 处的平均差为最小平均差,所以返回 3 。
|
示例 2:
1
2
3
4
5
| 输入:nums = [0]
输出:0
解释:
唯一的下标是 0 ,所以我们返回 0 。
下标 0 处的平均差为:|0 / 1 - 0| = |0 - 0| = 0 。
|
提示:
1 <= nums.length <= 10^50 <= nums[i] <= 10^5
解题思路
枚举分割点,利用前缀和计算区间和即可
注意前缀和的数据范围可能会超int
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public:
long long abs(long long a){
if(a>0) return a;
else return -a;
}
int minimumAverageDifference(vector<int>& nums) {
if(nums.size()==1) return 0;
vector<long long> dis(nums.size());
dis[0] = nums[0];
for(int i=1;i<nums.size();i++) dis[i] = dis[i-1]+nums[i];
long long sum = dis[nums.size()-1];
int idx=0;
long long minValue=0x3f3f3f3f,cur;
for(int i=0;i<nums.size();i++){
if(i==nums.size()-1) cur = abs(sum/nums.size());
else{
cur = abs(1LL*dis[i]/(i+1)-1LL*(sum-dis[i])/(nums.size()-i-1));
}
// cout<<cur<<endl;
if(cur<minValue){
minValue = cur;
idx = i;
}
}
return idx;
}
};
|
【模拟】统计网格中没有被保卫的格子数
题目
给你两个整数 m 和 n 表示一个下标从 0 开始的 m x n 网格图。同时给你两个二维整数数组 guards 和 walls ,其中 guards[i] = [rowi, coli] 且 walls[j] = [rowj, colj] ,分别表示第 i 个警卫和第 j 座墙所在的位置。
一个警卫能看到 4 个坐标轴方向(即东、南、西、北)的 所有 格子,除非他们被一座墙或者另外一个警卫 挡住 了视线。如果一个格子能被 至少 一个警卫看到,那么我们说这个格子被 保卫 了。
请你返回空格子中,有多少个格子是 没被保卫 的。
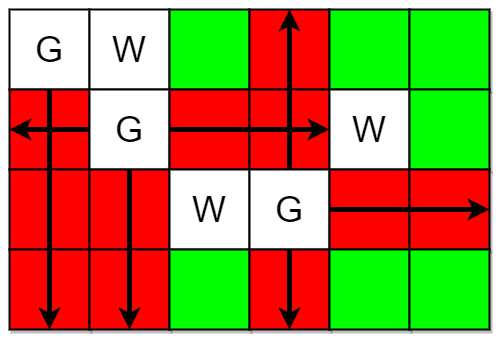
示例 1:
1
2
3
4
| 输入:m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]
输出:7
解释:上图中,被保卫和没有被保卫的格子分别用红色和绿色表示。
总共有 7 个没有被保卫的格子,所以我们返回 7 。
|
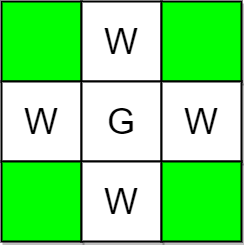
示例 2:
1
2
3
4
| 输入:m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]]
输出:4
解释:上图中,没有被保卫的格子用绿色表示。
总共有 4 个没有被保卫的格子,所以我们返回 4 。
|
提示:
1 <= m, n <= 10^52 <= m * n <= 10^51 <= guards.length, walls.length <= 5 * 10^42 <= guards.length + walls.length <= m * nguards[i].length == walls[j].length == 20 <= rowi, rowj < m0 <= coli, colj < nguards 和 walls 中所有位置 互不相同 。
解题思路
比赛的时候这题一开始通过率很高啊,第一眼看以为要用DFS做,后来看四个方向是一条路走到黑的,就想着模拟就好了
这题注意到数据规模了,mn不超过10^5,但是复杂度想错了
想着是枚举每一个警卫,然后对每个警卫的4个方向进行遍历,直到碰到墙或出界,以为会超时,时间复杂度最坏可能达到10^9。
需要想清楚的是,其实每个点最多被扫4次就够了
看到一个比喻:
5个人大家朝着同一个站成一队,你站在队伍的第4个位置,此时你会看到前方的人的后背;在这个情况下,站在你前面的人相当于替你看了前面的风景;
所以其实复杂度O(nm)就解决了这题
偷学代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
public:
int countUnguarded(int m, int n, vector<vector<int>>& gs, vector<vector<int>>& ws) {
vector<vector<int> > g(m, vector<int>(n, 0));
const int guard = 1;
const int wall = 2;
for (int i = 0; i < gs.size(); ++i) {
int x = gs[i][0], y = gs[i][1];
g[x][y] = guard;
}
for (int i = 0; i < ws.size(); ++i) {
int x = ws[i][0], y = ws[i][1];
g[x][y] = wall;
}
const int dx[4] = {1, -1, 0, 0};
const int dy[4] = {0, 0, 1, -1};
for (int i = 0; i < gs.size(); ++i) {
int x = gs[i][0], y = gs[i][1];
int xx, yy;
for (int d = 0; d < 4; ++d) {
for (int j = 1; ; ++j) {
xx = x + dx[d] * j; yy = y + dy[d] * j;
if (xx < 0 || xx >= m || yy < 0 || yy >= n || g[xx][yy] == guard || g[xx][yy] == wall) {
break;
}
g[xx][yy] = 3;
}
}
}
int res = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (g[i][j] == 0) {
++res;
}
}
}
return res;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| class Solution {
public:
int countUnguarded(int m, int n, vector<vector<int>>& guards, vector<vector<int>>& walls) {
vector<vector<int>> grid(m,vector<int>(n,0));
for(auto v:guards) grid[v[0]][v[1]]=1;
for(auto v:walls) grid[v[0]][v[1]]=2;
vector<vector<bool>> f(m,vector<bool>(n,false));
for(int i=0;i<m;i++){
bool t=false;
for(int j=0;j<n;j++){
if(grid[i][j]==1) t=true;
else if(grid[i][j]==2) t=false;
if(t) f[i][j]=true;
}
t=false;
for(int j=n-1;j>=0;j--){
if(grid[i][j]==1) t=true;
else if(grid[i][j]==2) t=false;
if(t) f[i][j]=true;
}
}
for(int j=0;j<n;j++){
bool t=false;
for(int i=0;i<m;i++)
{
if(grid[i][j]==1) t=true;
else if(grid[i][j]==2) t=false;
if(t) f[i][j]=true;
}
t=false;
for(int i=m-1;i>=0;i--){
if(grid[i][j]==1) t=true;
else if(grid[i][j]==2) t=false;
if(t) f[i][j]=true;
}
}
int ans=0;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++){
if(grid[i][j]==0&&!f[i][j]) ans++;
}
return ans;
}
};
|
另一种思路
比赛中后来我用的是另外一种思路
考虑每一个网格,找到它四个方向最近的物体,如果有警卫,就说明被保护到了
找最近的物体,可以对排序后的数组进行二分查找即可
这样的时间复杂度是O(n*m*max(log m, log n)),比前一种方法复杂度高
比赛的时候写麻了,变量整太多,没写注释都忘记啥意思了,然后一直编译错误,结束后冷静整理了一下一次过了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| #define P pair<int,int>
class Solution {
public:
int m,n;//m行n列
vector<vector<int>> G,W,grid;
bool rfun(int row, int col, vector<int>& arr){//行坐标,列坐标,网格[row,col]能否被第row行的警卫看到
auto idx_max = upper_bound(arr.begin(),arr.end(),col);
if(idx_max != arr.end()){
if(grid[row][*idx_max]==2) return true;
}
auto idx_min = lower_bound(arr.begin(),arr.end(),col);
if(idx_min!=arr.begin()){
if(grid[row][*(--idx_min)]==2) return true;
}
return false;
}
bool cfun(int row, int col, vector<int>& arr){//行坐标,列坐标,网格[row,col]能否被第col列的警卫看到
auto idx_max = upper_bound(arr.begin(),arr.end(),row);
if(idx_max != arr.end()){
if(grid[*idx_max][col]==2) return true;
}
auto idx_min = lower_bound(arr.begin(),arr.end(),row);
if(idx_min!=arr.begin()){
if(grid[*(--idx_min)][col]==2) return true;
}
return false;
}
int countUnguarded(int m, int n, vector<vector<int>>& guards, vector<vector<int>>& walls) {
this->m = m;
this->n = n;
G=guards,W=walls;
grid.resize(m);
for(int i=0;i<m;i++) grid[i].resize(n,0);
//r[i] 行坐标为i的 警卫、墙的列数组
//c[i] 列坐标为i的 警卫、墙的行数组
unordered_map< int,vector<int> > r,c;
for(auto &x:walls){
grid[x[0]][x[1]] = 1;
r[x[0]].push_back(x[1]);//列坐标
c[x[1]].push_back(x[0]);
}
for(auto &x:guards){
grid[x[0]][x[1]] = 2;
r[x[0]].push_back(x[1]);
c[x[1]].push_back(x[0]);
}
//排序以用于二分查找
for(auto &x:r){
sort(x.second.begin(),x.second.end());
}
for(auto &x:c){
sort(x.second.begin(),x.second.end());
}
int res = 0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]) continue;
if(rfun(i,j,r[i])) {//网格[i][j]在第i行上有被警卫保护
}else if(cfun(i,j,c[j])){//网格[i][j]在第j列上有被警卫保护
}else{
res++;
}
}
}
return res;
}
};
|
【二分+BFS】逃离火灾
题目
给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ,它表示一个网格图。每个格子为下面 3 个值之一:
0 表示草地。1 表示着火的格子。2 表示一座墙,你跟火都不能通过这个格子。
一开始你在最左上角的格子 (0, 0) ,你想要到达最右下角的安全屋格子 (m - 1, n - 1) 。每一分钟,你可以移动到 相邻 的草地格子。每次你移动 之后 ,着火的格子会扩散到所有不是墙的 相邻 格子。
请你返回你在初始位置可以停留的 最多 分钟数,且停留完这段时间后你还能安全到达安全屋。如果无法实现,请你返回 -1 。如果不管你在初始位置停留多久,你 总是 能到达安全屋,请你返回 109 。
注意,如果你到达安全屋后,火马上到了安全屋,这视为你能够安全到达安全屋。
如果两个格子有共同边,那么它们为 相邻 格子。
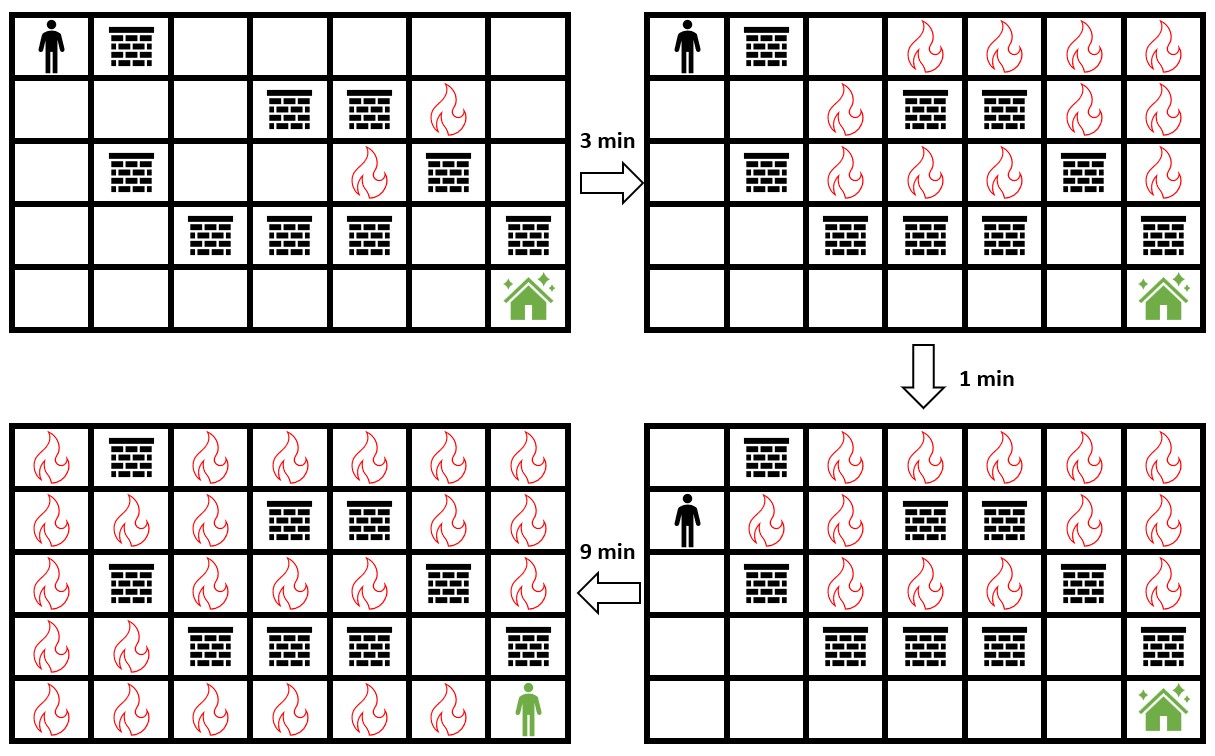
示例 1:
1
2
3
4
5
| 输入:grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]]
输出:3
解释:上图展示了你在初始位置停留 3 分钟后的情形。
你仍然可以安全到达安全屋。
停留超过 3 分钟会让你无法安全到达安全屋。
|
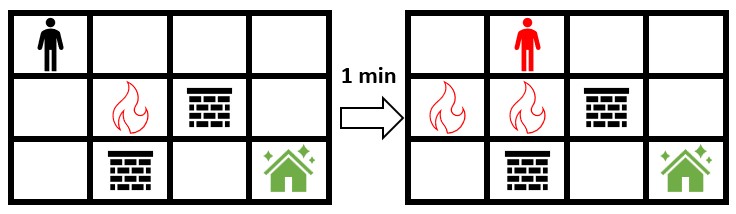
示例 2:
1
2
3
4
5
| 输入:grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]]
输出:-1
解释:上图展示了你马上开始朝安全屋移动的情形。
火会蔓延到你可以移动的所有格子,所以无法安全到达安全屋。
所以返回 -1 。
|
示例 3:
1
2
3
4
5
| 输入:grid = [[0,0,0],[2,2,0],[1,2,0]]
输出:1000000000
解释:上图展示了初始网格图。
注意,由于火被墙围了起来,所以无论如何你都能安全到达安全屋。
所以返回 109 。
|
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 3004 <= m * n <= 2 * 10^4grid[i][j] 是 0 ,1 或者 2 。grid[0][0] == grid[m - 1][n - 1] == 0
解题思路
首先利用BFS预处理火势蔓延所需要的最小时间
然后二分答案t
利用BFS判断在原地停留t时间后,能否安全到达安全屋
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| class Solution {
public:
int dir[4][2]={ {-1,0},{1,0},{0,-1},{0,1} };
int maximumMinutes(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
vector<vector<int>> f(n,vector<int>(m,INT_MAX));
queue<pair<int,int>> q;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
if(grid[i][j]==1) f[i][j]=0,q.emplace(i,j);
auto bound = [&](int x, int y){
if(x<0||x>=n) return false;
if(y<0||y>=m) return false;
return true;
};
while(!q.empty()){//spread fire
auto [x,y] = q.front();
q.pop();
for(int i=0;i<4;i++){
int dx=x+dir[i][0],dy=y+dir[i][1];
if(!bound(dx,dy)) continue;
if(f[dx][dy]!=INT_MAX) continue;
if(grid[dx][dy]==2) continue;
f[dx][dy] = f[x][y]+1;
q.emplace(dx,dy);
}
}
//f[i][j] 火蔓延至[i][j]的最短时间
//d[i][j] 人移动到[i][j]的最短时间
auto check = [&](int t){//等待t时间后是否安全
vector<vector<int>> d(n,vector<int>(m,INT_MAX));
d[0][0] = t;//原地等t时间
queue<pair<int,int>> que;
que.emplace(0,0);
while(!que.empty()){
auto [x,y] = que.front();que.pop();
for(int i=0;i<4;i++){
int dx = x+dir[i][0];
int dy = y+dir[i][1];
if(!bound(dx,dy)) continue;
if(grid[dx][dy]==2) continue;
if(d[dx][dy]!=INT_MAX) continue;
d[dx][dy] = d[x][y] + 1;
if(dx==n-1 && dy==m-1){//移动到安全屋时
if(d[dx][dy]<=f[dx][dy]) return true;
else return false;
}
if(d[dx][dy]>=f[dx][dy]) {}//中途被烧,放弃这条路
else que.emplace(dx,dy);//这条路没被烧,继续走
}
}
return false;//到不了安全屋,或是所有路在中途都会被烧
};
int l=0,r=1e9+1;//左闭右开
while(l<r){
int mid = l+r>>1;
if(check(mid)) l=mid+1;//如果可以停留mid时间,右移左边界,尝试增加时间
else r=mid;
}
//l-1
return l-1;
}
};
|






