Featured image of post LeetCode第78场双周赛总结
leetcode contest

LeetCode第78场双周赛总结

330/4347

image-20220515162208775

上大分上大分，刷新个人最好排名（虽然后面周赛又刷新了）

5/18更新：不知怎么的，排名上升了。最好排名再度刷新。

image-20220518122143179

【模拟】找到一个数字的 K 美丽值

题目

一个整数 num 的 k 美丽值定义为 num 中符合以下条件的 子字符串 数目：

  • 子字符串长度为 k 。
  • 子字符串能整除 num 。

给你整数 num 和 k ，请你返回 num 的 k 美丽值。

注意：

  • 允许有 前缀 0 。
  • 0 不能整除任何值。

一个 子字符串 是一个字符串里的连续一段字符序列。

示例 1：

1
2
3
4
5
6

输入：num = 240, k = 2
输出：2
解释：以下是 num 里长度为 k 的子字符串：
- "240" 中的 "24" ：24 能整除 240 。
- "240" 中的 "40" ：40 能整除 240 。
所以，k 美丽值为 2 。

示例 2：

1
2
3
4
5
6
7
8
9

输入：num = 430043, k = 2
输出：2
解释：以下是 num 里长度为 k 的子字符串：
- "430043" 中的 "43" ：43 能整除 430043 。
- "430043" 中的 "30" ：30 不能整除 430043 。
- "430043" 中的 "00" ：0 不能整除 430043 。
- "430043" 中的 "04" ：4 不能整除 430043 。
- "430043" 中的 "43" ：43 能整除 430043 。
所以，k 美丽值为 2 。

提示：

  • 1 <= num <= 10^9
  • 1 <= k <= num.length （将 num 视为字符串）

解题思路

按题意模拟即可。

这次用着to_string和stoi函数，写代码提速不少

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
public:
    int divisorSubstrings(int num, int k) {
        string str = to_string(num);
        int n = str.size(), res = 0;
        for(int i=0;i+k<=n;i++){
            int cur = stoi(str.substr(i,k));
            if(cur==0) continue;
            if(num%cur==0) res++;
        }
        return res;
    }
};

【枚举+前缀和】分割数组的方案数

题目

给你一个下标从 0 开始长度为 n 的整数数组 nums 。 如果以下描述为真，那么 nums 在下标 i 处有一个 合法的分割 ：

  • 前 i + 1 个元素的和 大于等于 剩下的 n - i - 1 个元素的和。
  • 下标 i 的右边 至少有一个 元素，也就是说下标 i 满足 0 <= i < n - 1 。

请你返回 nums 中的 合法分割 方案数。

示例 1：

1
2
3
4
5
6
7
8

输入：nums = [10,4,-8,7]
输出：2
解释：
总共有 3 种不同的方案可以将 nums 分割成两个非空的部分：
- 在下标 0 处分割 nums 。那么第一部分为 [10] ，和为 10 。第二部分为 [4,-8,7] ，和为 3 。因为 10 >= 3 ，所以 i = 0 是一个合法的分割。
- 在下标 1 处分割 nums 。那么第一部分为 [10,4] ，和为 14 。第二部分为 [-8,7] ，和为 -1 。因为 14 >= -1 ，所以 i = 1 是一个合法的分割。
- 在下标 2 处分割 nums 。那么第一部分为 [10,4,-8] ，和为 6 。第二部分为 [7] ，和为 7 。因为 6 < 7 ，所以 i = 2 不是一个合法的分割。
所以 nums 中总共合法分割方案受为 2 。

示例 2：

1
2
3
4
5
6

输入：nums = [2,3,1,0]
输出：2
解释：
总共有 2 种 nums 的合法分割：
- 在下标 1 处分割 nums 。那么第一部分为 [2,3] ，和为 5 。第二部分为 [1,0] ，和为 1 。因为 5 >= 1 ，所以 i = 1 是一个合法的分割。
- 在下标 2 处分割 nums 。那么第一部分为 [2,3,1] ，和为 6 。第二部分为 [0] ，和为 0 。因为 6 >= 0 ，所以 i = 2 是一个合法的分割。

提示：

  • 2 <= nums.length <= 10^5
  • -105 <= nums[i] <= 10^5

解题思路

预先计算好前缀和，计算判断即可

注意数据范围，可能超int。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution {
public:
    int waysToSplitArray(vector<int>& nums) {
        int n = nums.size();
        vector<long long> sum(n+1,0);
        for(int i=1;i<=n;i++){
            sum[i] = sum[i-1]+nums[i-1];
        }
        int res = 0;
        for(int i=1;i<n;i++){
            if(sum[i]>=sum[n]-sum[i]) res++;
        }
        return res;
    }
};

【动态开点线段树】毯子覆盖的最多白色砖块数

题目

给你一个二维整数数组 tiles ，其中 tiles[i] = [li, ri] ，表示所有在 li <= j <= ri 之间的每个瓷砖位置 j 都被涂成了白色。

同时给你一个整数 carpetLen ，表示可以放在 任何位置 的一块毯子。

请你返回使用这块毯子，最多 可以盖住多少块瓷砖。

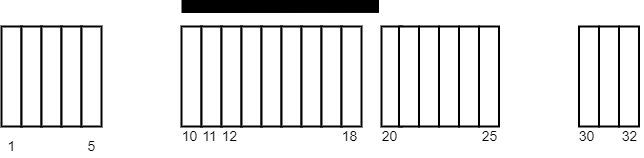
示例 1：

img

1
2
3
4
5
6

输入：tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
输出：9
解释：将毯子从瓷砖 10 开始放置。
总共覆盖 9 块瓷砖，所以返回 9 。
注意可能有其他方案也可以覆盖 9 块瓷砖。
可以看出，瓷砖无法覆盖超过 9 块瓷砖。

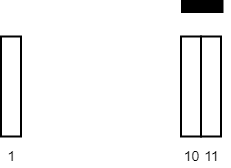
示例 2：

img

1
2
3
4

输入：tiles = [[10,11],[1,1]], carpetLen = 2
输出：2
解释：将毯子从瓷砖 10 开始放置。
总共覆盖 2 块瓷砖，所以我们返回 2 。

提示：

  • 1 <= tiles.length <= 5 * 10^4
  • tiles[i].length == 2
  • 1 <= li <= ri <= 10^9
  • 1 <= carpetLen <= 10^9
  • tiles 互相 不会重叠 。

解题思路

首先可以预处理判断是否存在长度大于等于毛毯长度的瓷砖区间，若存在，直接返回毛毯长度即可。

更一般地，一个长度单位的毛毯最多覆盖一个长度单位的瓷砖，所以每次将毛毯的末尾对准瓷砖区间[l , r]的r（右端点），考虑此时毛毯的起始位置pos（>=1，r+1-carpetLen），如果pos>=l，即毛毯可以被瓷砖”填满“，答案为carpetLen（即上述预处理的情况）；如果pos<l，此时[pos, l-1]处有瓷砖就加上，答案为[pos, r]区间内的瓷砖个数（前一种也是这样）。

其实也就可以看成一个区间修改，区间求和问题，注意到值域的范围达到了10^9，但询问次数范围为5*10^4，所以要采用动态开点线段树。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

const int MAXM = 4e6+6;
const int INF = 1e9+5;
class Solution {
public:
    int tot,root;
    struct node{
        int sum;
        int tag;
        int ls,rs;
    }T[MAXM];
    void push_up(int& p){
        T[p].sum = T[T[p].ls].sum + T[T[p].rs].sum;
    }
    void push_down(int &p, int l, int r){
        if(!T[p].tag) return;
        if(!T[p].ls){
            T[p].ls=++tot;
            T[T[p].ls]={0,0,0,0};
        }
        if(!T[p].rs){
            T[p].rs=++tot;
            T[T[p].rs]={0,0,0,0};
        }
        int mid=(l+r)>>1;
        T[T[p].ls].tag+=T[p].tag;
        T[T[p].rs].tag+=T[p].tag;
        T[T[p].ls].sum += T[p].tag*(mid-l+1);
        T[T[p].rs].sum += T[p].tag*(r-mid);
        T[p].tag=0;
    }
    void update(int& p, int l, int r, int nl, int nr, int k){
        if(!p){
            p=++tot;
            T[p]={0,0,0,0};
        }
        if(nl<=l && nr>=r){
            T[p].sum = k*(r-l+1);
            T[p].tag = k;
            return;
        }
        int mid=(l+r)>>1;
        push_down(p,l,r);
        if(nl<=mid) update(T[p].ls, l, mid,nl,nr,k);
        if(nr>mid) update(T[p].rs,mid+1,r,nl,nr,k);
        push_up(p);
    }
    int query(int p, int l, int r, int nl, int nr){
        if(nl<=l&&nr>=r) return T[p].sum;
        long long res = 0;
        int mid = (l+r)>>1;
        push_down(p,l,r);
        if(nl<=mid) res+=query(T[p].ls,l,mid,nl,nr);
        if(nr>mid) res+=query(T[p].rs,mid+1,r,nl,nr);
        return res;
    }
    
    int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) {
       
        tot=0,root=0;
       
        int maxlen=-1;
        for(auto &vec: tiles){
            maxlen=max(maxlen,vec[1]-vec[0]+1);
            
        }
        if(maxlen>=carpetLen) return carpetLen;
        for(auto &vec: tiles){
            update(root,1,INF,vec[0],vec[1],1);
        }
        
        for(auto &vec: tiles){
            int r = vec[1];
            int l = max(1,r+1-carpetLen);
            maxlen = max(maxlen, query(root,1,INF,l,r));
        }
        
        return maxlen;
    }
};

贪心+滑动窗口

枚举毯子的左端点和哪组瓷砖的左端点一致，并通过滑动窗口维护此时毯子右边最多覆盖到哪组瓷砖，取最大值作为答案即可

枚举第i组瓷砖的左端点，窗口左边界i表示第i组瓷砖，右边界j随着毯子能覆盖的范围而增加，维护一个变量now记录当前毯子能覆盖的瓷砖范围。

毯子无法完全覆盖第j组瓷砖时，有两种情况，1）碰都碰不到第j组瓷砖，此时加上0；2）可以碰到，此时可以覆盖部分，长度为：毛毯此时右端点 tiles[i][0]+carpetLen-1，第j组子串左端点 tiles[j][0]，前者减后者再加1。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) {
        sort(tiles.begin(), tiles.end());
        long long now = 0, ans = 0;
        for (int i = 0, j = 0; i < tiles.size(); i++) {
            while (j < tiles.size() && tiles[j][1] + 1 - tiles[i][0] <= carpetLen) now += tiles[j][1] - tiles[j][0] + 1, j++;
            // 毯子无法完全覆盖第 j 组瓷砖
            if (j < tiles.size()) ans = max(ans, now + max(0, tiles[i][0] + carpetLen - tiles[j][0]));
            // 毯子可以完全覆盖第 j 组瓷砖
            else ans = max(ans, now);
            now -= tiles[i][1] - tiles[i][0] + 1;//减去第i组瓷砖
        }
        return ans;
    }
};

// 作者：TsReaper
// 链接：https://leetcode.cn/circle/discuss/Mmxf4g/
// 来源：力扣（LeetCode）
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

【枚举+动态规划】最大波动的子字符串

题目

字符串的 波动 定义为子字符串中出现次数 最多 的字符次数与出现次数 最少 的字符次数之差。

给你一个字符串 s ，它只包含小写英文字母。请你返回 s 里所有 子字符串的 最大波动 值。

子字符串 是一个字符串的一段连续字符序列。

示例 1：

1
2
3
4
5
6
7
8
9

输入：s = "aababbb"
输出：3
解释：
所有可能的波动值和它们对应的子字符串如以下所示：
- 波动值为 0 的子字符串："a" ，"aa" ，"ab" ，"abab" ，"aababb" ，"ba" ，"b" ，"bb" 和 "bbb" 。
- 波动值为 1 的子字符串："aab" ，"aba" ，"abb" ，"aabab" ，"ababb" ，"aababbb" 和 "bab" 。
- 波动值为 2 的子字符串："aaba" ，"ababbb" ，"abbb" 和 "babb" 。
- 波动值为 3 的子字符串 "babbb" 。
所以，最大可能波动值为 3 。

示例 2：

1
2
3
4

输入：s = "abcde"
输出：0
解释：
s 中没有字母出现超过 1 次，所以 s 中每个子字符串的波动值都是 0 。

提示：

  • 1 <= s.length <= 10^4
  • s 只包含小写英文字母。

解题思路

这次双周赛交完第3题看排名是三百多，太兴奋了，看完第4题，想到用动态规划做，思考了一会儿无果就放弃了。

结束后看题解，这个枚举就很灵性，妙！找出变化范围少的变量，枚举固定它，以更好地观察其他变化范围更大的变量。

枚举出现次数最多的字符和出现次数最少的字符，出现最多的字符每个贡献1，出现最少的字符每个贡献-1，其他字符可以忽略（看作0即可），将原数组转换成1，0，-1的序列a，此时，问题就转换成了，求最大子序和了（且至少含有1和-1两种不同元素）。

令dp[i]表示以a[i]结尾的最大子序和（即常规子序和），初始化dp[0]=a[0]，递归关系为dp[i]=(dp[i-1]+a[i], a[i])，最大的子序和为转移过程中的最大值。

为了保证子字符串中存在两种以上（含）的字符，即转换后的子数组中至少含有1和-1两种不同元素，令dp2[i]表示以a[i]结尾且至少含一个元素-1的最大子序和。不用管含不含元素1，含了最好，不含的话最大子序和一定也大不过最优解。

初始化dp2[0]要分情况讨论，如果a[0]=-1，满足条件，那么dp2[0]=a[0]；如果a[0]!=-1，那么不存在，令dp2[0]=-INF，其中-INF表示”无穷小“。

转移过程：

1
2
3
4
5

if(a[i]==-1){
    dp2[i]=max(dp2[i-1]+a[i], max(dp[i-1]+a[i], a[i]));//第i个元素为-1，那么前i-1个可以含或者不含，取最大值
}else{
    dp2[i]=dp2[i-1]+a[i];//只能寄希望于前i-1个元素含-1了
}

最后答案即为转移过程中的最大值

最大子序和（至少含一个-1）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

const int INF = 0x3f3f3f3f;
class Solution {
public:
    
    int largestVariance(string s) {
        int n = s.size();
        if(n==1) return 0;
        int res=0;
        int dp[n],dp2[n];
        for(char high='a';high<='z';high++){//枚举出现最多字符次数
            for(char low='a';low<='z';low++){//枚举出现最少字符次数
                if(high==low) continue;
                //highchar = 1; lowchar = -1
                memset(dp,0,sizeof(dp));
                memset(dp2,0,sizeof(dp));
                //dp[i]：以a[i]结尾的最大子数组和
                //dp2[i]：以a[i]结尾且至少含一个-1的最大子数组和
                int a0=(s[0]==high)?1:((s[0]==low)?-1:0);
                dp[0]=a0;
                dp2[0]=a0==-1?-1:-INF;
                for(int i=1;i<n;i++){
                    int v = (s[i]==high)?1:((s[i]==low)?-1:0);//a[i]
                    dp[i] = max(dp[i-1]+v, v);
                    if(v!=-1){
                        dp2[i]=dp2[i-1]+v;
                    }else{
                        dp2[i]=max(dp[i-1]+v,max(dp2[i-1]+v,v));
                    }
                    res = max(res, dp2[i]);
                }
            }
        }
        return res;
    }
};

空间优化

由于两个dp数组都只与前一个相关，因此可以省去第一维，进行空间优化，注意dp2会用到前一个的dp，所以dp后更改

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

const int INF = 0x3f3f3f3f;
class Solution {
public:
    int largestVariance(string s) {
        int n = s.size();
        if(n==1) return 0;
        int res=0;
        for(char high='a';high<='z';high++){//枚举出现最多字符次数
            for(char low='a';low<='z';low++){//枚举出现最少字符次数
                if(high==low) continue;
                //highchar = 1; lowchar = -1
                int dp,dp2;
                int a0=(s[0]==high)?1:((s[0]==low)?-1:0);
                dp=a0;
                dp2=a0==-1?-1:-INF;
                for(int i=1;i<n;i++){
                    int v = (s[i]==high)?1:((s[i]==low)?-1:0);
                    if(v!=-1){
                        dp2=dp2+v;
                    }else{
                        dp2=max(dp+v,max(dp2+v,v));
                    }
                    dp = max(dp+v, v);
                    res = max(res, dp2);
                }
            }
        }
        return res;
    }
};

关于运行时间

最开始我在循环内将dp数组定义为vector，26*26次枚举的初始化，第一次提交超时了，因为vector初始化什么的太慢了，超时的那个数据规模为10^4。

然后改成普通数组，并将其定义放到循环外，循环内用memset进行初始化，速度快了不少。

以后涉及到多次数组初始化的话，还是避免使用vector吧，效率太低了。

image-20220516121641970

空间优化后，避免了多次数组的初始化，时间也得到了提升。

常规动态规划

如果不从最大子序和的角度出发的话：

设a为最多字符，b为最少字符。 dp[0]表示当前位置结尾的，连续a字符的数量 dp[1]表示当前位置结尾的最大波动值

如果仅仅定义表示当前位置结尾的最大波动值的变量是不够的，还需要一个辅助计数的变量，考虑如果还没出现b的时候，应该存储什么呢？

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
public:
    int largestVariance(string s) {
        int n = s.size(), ans = 0;
        for(char a = 'a'; a <= 'z'; ++a){
            for(char b = 'a'; b <= 'z'; ++b){
                if(a == b) continue;
                int dp[2]{0,-114514};
                for(char c: s){
                    if(c == b) {
                        dp[1] = max(dp[1] - 1, dp[0] - 1);
                        dp[0] = 0;
                    }
                    else if(c == a){
                        ++dp[0], ++dp[1];
                    }
                    ans = max(ans, dp[1]);
                }
            }
        }
        return ans;
    }
};

作者：MuriyaTensei
链接：https://leetcode.cn/problems/substring-with-largest-variance/solution/c-dong-tai-gui-hua-by-muriyatensei-nuux/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
动态规划
Licensed under CC BY-NC-SA 4.0
Last updated on May 16, 2022 00:00 UTC
© 2020 - 2024 おう てつ の blog
Built with Hugo
Theme Stack designed by Jimmy