LeetCode第79场双周赛总结

# 【模拟】判断一个数的数字计数是否等于数位的值

# 题目

给你一个下标从 0 开始长度为 n 的字符串 num ，它只包含数字。

如果对于每个 0 <= i < n 的下标 i ，都满足数位 i 在 num 中出现了 num[i]次，那么请你返回 true ，否则返回 false 。

示例 1：

1
2
3
4
5
6
7
8
输入：num = "1210"
输出：true
解释：
num[0] = '1' 。数字 0 在 num 中出现了一次。
num[1] = '2' 。数字 1 在 num 中出现了两次。
num[2] = '1' 。数字 2 在 num 中出现了一次。
num[3] = '0' 。数字 3 在 num 中出现了零次。
"1210" 满足题目要求条件，所以返回 true 。

示例 2：

1
2
3
4
5
6
7
输入：num = "030"
输出：false
解释：
num[0] = '0' 。数字 0 应该出现 0 次，但是在 num 中出现了一次。
num[1] = '3' 。数字 1 应该出现 3 次，但是在 num 中出现了零次。
num[2] = '0' 。数字 2 在 num 中出现了 0 次。
下标 0 和 1 都违反了题目要求，所以返回 false 。

提示：

n == num.length
1 <= n <= 10
num 只包含数字。

# 解题思路

模拟即可

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Solution {
public:
    bool digitCount(string num) {
        vector<int> a(10,0);//a[i]  i出现的次数
        for(auto &x: num){
            a[x-'0']++;
        }
        for(int i=0;i<num.size();i++){
            
            if(a[i]!=num[i]-'0') return false;
        }
        return true;
    }
};

# 【模拟】最多单词数的发件人

# 题目

给你一个聊天记录，共包含 n 条信息。给你两个字符串数组 messages 和 senders ，其中 messages[i] 是 senders[i] 发出的一条信息。

一条信息是若干用单个空格连接的单词，信息开头和结尾不会有多余空格。发件人的 单词计数 是这个发件人总共发出的 单词数 。注意，一个发件人可能会发出多于一条信息。

请你返回发出单词数最多的发件人名字。如果有多个发件人发出最多单词数，请你返回 字典序 最大的名字。

注意：

字典序里，大写字母小于小写字母。
"Alice" 和 "alice" 是不同的名字。

示例 1：

1
2
3
4
5
6
输入：messages = ["Hello userTwooo","Hi userThree","Wonderful day Alice","Nice day userThree"], senders = ["Alice","userTwo","userThree","Alice"]
输出："Alice"
解释：Alice 总共发出了 2 + 3 = 5 个单词。
userTwo 发出了 2 个单词。
userThree 发出了 3 个单词。
由于 Alice 发出单词数最多，所以我们返回 "Alice" 。

示例 2：

1
2
3
4
5
输入：messages = ["How is leetcode for everyone","Leetcode is useful for practice"], senders = ["Bob","Charlie"]
输出："Charlie"
解释：Bob 总共发出了 5 个单词。
Charlie 总共发出了 5 个单词。
由于最多单词数打平，返回字典序最大的名字，也就是 Charlie 。

提示：

n == messages.length == senders.length
1 <= n <= 10^4
1 <= messages[i].length <= 100
1 <= senders[i].length <= 10
messages[i] 包含大写字母、小写字母和 ' ' 。
messages[i] 中所有单词都由 单个空格 隔开。
messages[i] 不包含前导和后缀空格。
senders[i] 只包含大写英文字母和小写英文字母。

# 解题思路

统计每个人发送的单词个数

WA了一发，WA在返回值的初始化上，不能盲目地像整型那样，直接初始化答案为第1个人是不妥的。

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int fun(string s){
        int res=0;
        for(auto &x: s){
            if(x==' ') res++;
        }
        return res+1;
    }
    string largestWordCount(vector<string>& messages, vector<string>& senders) {
        
        int maxnum = 0;
        int n = messages.size();
        map<string,int> tab;
        for(int i=0;i<n;i++){
            tab[senders[i]] += fun(messages[i]);
        }
        string res = "";
        for(auto &x: tab){
            // cout<<x.first<<' '<<x.second<<' '<<maxnum<<endl;
            if(x.second>=maxnum){
                // cout<<"   "<<res<<endl;
                maxnum = x.second;
                if(x.first>=res) res = x.first;
            }
        }
        return res;
    }
};

# 【贪心】道路的最大总重要性

# 题目

给你一个整数 n ，表示一个国家里的城市数目。城市编号为 0 到 n - 1 。

给你一个二维整数数组 roads ，其中 roads[i] = [ai, bi] 表示城市 ai 和 bi 之间有一条双向道路。

你需要给每个城市安排一个从 1 到 n 之间的整数值，且每个值只能被使用一次。道路的 重要性 定义为这条道路连接的两座城市数值之和。

请你返回在最优安排下，所有道路重要性 之和最大为多少。

示例 1：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
输入：n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
输出：43
解释：上图展示了国家图和每个城市被安排的值 [2,4,5,3,1] 。
- 道路 (0,1) 重要性为 2 + 4 = 6 。
- 道路 (1,2) 重要性为 4 + 5 = 9 。
- 道路 (2,3) 重要性为 5 + 3 = 8 。
- 道路 (0,2) 重要性为 2 + 5 = 7 。
- 道路 (1,3) 重要性为 4 + 3 = 7 。
- 道路 (2,4) 重要性为 5 + 1 = 6 。
所有道路重要性之和为 6 + 9 + 8 + 7 + 7 + 6 = 43 。
可以证明，重要性之和不可能超过 43 。

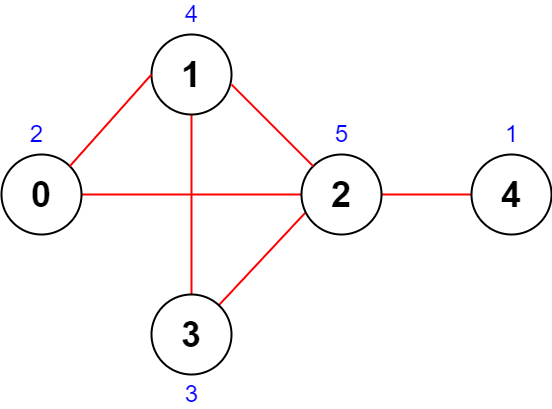
示例 2：

1
2
3
4
5
6
7
8
输入：n = 5, roads = [[0,3],[2,4],[1,3]]
输出：20
解释：上图展示了国家图和每个城市被安排的值 [4,3,2,5,1] 。
- 道路 (0,3) 重要性为 4 + 5 = 9 。
- 道路 (2,4) 重要性为 2 + 1 = 3 。
- 道路 (1,3) 重要性为 3 + 5 = 8 。
所有道路重要性之和为 9 + 3 + 8 = 20 。
可以证明，重要性之和不可能超过 20 。

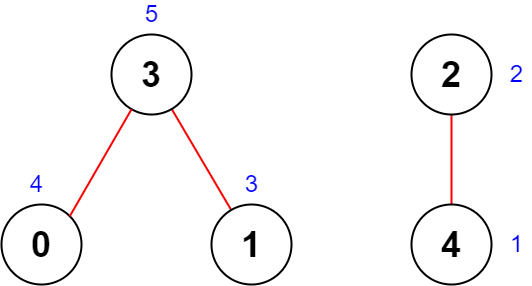
提示：

2 <= n <= 5 * 10^4
1 <= roads.length <= 5 * 10^4
roads[i].length == 2
0 <= ai, bi <= n - 1
ai != bi
没有重复道路。

# 解题思路

显然对邻居数越多的点赋予越重要的值，收益越大

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    long long maximumImportance(int n, vector<vector<int>>& roads) {
        long long res = 0;
        vector<int> cnt(n,0);
        for(auto &x: roads){
            cnt[x[0]]++;
            cnt[x[1]]++;
        }
        sort(cnt.begin(),cnt.end(),greater<int>());
        
        // for(auto &x: cnt) cout<<x<<' ';
        int a = n;
        for(auto &x: cnt){
            res += 1ll*a*x;
            a--;
        }
        return res;
    }
};

# 【线段树好题】以组为单位订音乐会的门票

# 题目

一个音乐会总共有 n 排座位，编号从 0 到 n - 1 ，每一排有 m 个座椅，编号为 0 到 m - 1 。你需要设计一个买票系统，针对以下情况进行座位安排：

同一组的 k 位观众坐在 同一排座位，且座位连续 。
k 位观众中 每一位 都有座位坐，但他们 不一定 坐在一起。

由于观众非常挑剔，所以：

只有当一个组里所有成员座位的排数都 小于等于 maxRow ，这个组才能订座位。每一组的 maxRow 可能不同。
如果有多排座位可以选择，优先选择最小的排数。如果同一排中有多个座位可以坐，优先选择号码最小的。

请你实现 BookMyShow 类：

BookMyShow(int n, int m) ，初始化对象，n 是排数，m 是每一排的座位数。
int[] gather(int k, int maxRow) 返回长度为 2 的数组，表示 k 个成员中 第一个座位 的排数和座位编号，这 k 位成员必须坐在 同一排座位，且座位连续 。换言之，返回最小可能的 r 和 c 满足第 r 排中 [c, c + k - 1] 的座位都是空的，且 r <= maxRow 。如果无法安排座位，返回 [] 。
boolean scatter(int k, int maxRow) 如果组里所有 k 个成员 不一定 要坐在一起的前提下，都能在第 0 排到第 maxRow 排之间找到座位，那么请返回 true 。这种情况下，每个成员都优先找排数最小，然后是座位编号最小的座位。如果不能安排所有 k 个成员的座位，请返回 false 。

示例 1：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
输入：
["BookMyShow", "gather", "gather", "scatter", "scatter"]
[[2, 5], [4, 0], [2, 0], [5, 1], [5, 1]]
输出：
[null, [0, 0], [], true, false]

解释：
BookMyShow bms = new BookMyShow(2, 5); // 总共有 2 排，每排 5 个座位。
bms.gather(4, 0); // 返回 [0, 0]
                  // 这一组安排第 0 排 [0, 3] 的座位。
bms.gather(2, 0); // 返回 []
                  // 第 0 排只剩下 1 个座位。
                  // 所以无法安排 2 个连续座位。
bms.scatter(5, 1); // 返回 True
                   // 这一组安排第 0 排第 4 个座位和第 1 排 [0, 3] 的座位。
bms.scatter(5, 1); // 返回 False
                   // 总共只剩下 2 个座位。

提示：

1 <= n <= 5 * 10^4
1 <= m, k <= 10^9
0 <= maxRow <= n - 1
gather 和 scatter 总调用次数不超过 5 * 10^4 次。

# 解题思路

比赛的时候这题一开始一直刷不出来？后面看到题也没有思路。就没去做了。看了题解码了代码，发现真是一道线段树好题。

想到了可能要用线段树，但不知道维护啥，当时没注意到座位排的每一行最左边都是排满的，即不会出现两边坐人，中间有空的情况，所以还是很方便维护的。

即线段树的叶子节点对应的是，第i排座位的使用情况，分析后面操作可知，区间维护总和和最大值即可。

题中共有两种操作，gather操作和scatter操作。

（由于写线段树一般都从1开始，所以与题中0开始的计序，有个1的偏移）

对于gather操作，对于区间[1,maxRow+1]，在该区间查询是否存在有某一个单点的剩余座位数大于等于k，如果存在，则需要对最左边这样的单点进行更新。这需要维护区间最大值（区间最大剩余座位数）。

对于scatter操作，对于区间[1,maxRow+1]，在该区间查询剩余总座位数是否大于等于k，如果满足，则需要从左到右落座，即从最左边开始对若干单点进行更新。这需要维护区间总和（区间剩余座位数的总和）。

1
2
3
4
struct node{
    ll sum;//区间内剩余座位的总和，可能溢出，定义类型为long long
    int maxv;//区间内最大剩余座位数
}T[MAXN<<2];

# push_up

1
2
3
4
void push_up(int p){
    T[p].sum = T[ls(p)].sum+T[rs(p)].sum;
    T[p].maxv = max(T[ls(p)].maxv, T[rs(p)].maxv);
}

更新总和以及最大值。

注意此题是用不到区间更新的，所以不需要用懒标记，即不需要push_down。

# build

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
void build(int p, int l, int r){
    T[p]={0,0};
    if(l==r){
    	T[p]={m,m};//初始时，单排剩余座位为m
    	return;
    }
    int mid=(l+r)>>1;
    build(ls(p),l,mid);
    build(rs(p),mid+1,r);
    push_up(p);
}

常规线段树建树。叶子节点对应的是单点，即每一排座位的情况。非叶子节点对应的是一个长度大于1的区间，维护了该区间内剩余座位的总和以及最大值。

# gather操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//gather 在[nl,nr]区间内查询第一个剩余座位大于等于k的单点
//如果找到，还要进行单点更新
vector<int> do_gather(int p, int l, int r, int nl, int nr, int k){
    if(T[p].maxv < k) return {};//最大容量都满足不了
    
    //l==r说明是单点 nr>=r&&nl<=l说明满足区间要求  找到解了
    if(l==r && nr>=r && nl<=l){
        vector<int> res(2,0);
        res[0] = l-1;
        res[1] = m-T[p].maxv;
        T[p].maxv -= k;//修改
        T[p].sum -= k;
        return res;
    }
    vector<int> ans;
    int mid=(l+r)>>1;
    //要么往左子树走要么往右子树走，直到叶子节点为止
    //如果左子树够的话，肯定先往左子树走；否则往右子树走
    if(T[ls(p)].maxv>=k && nl<=mid) ans = do_gather(ls(p),l,mid,nl,nr,k);
    else if(T[rs(p)].maxv>=k && nr>mid) ans = do_gather(rs(p),mid+1,r,nl,nr,k);
    push_up(p);
    return ans;
}

这个操作处理题中的gather操作。将区间查询和单点更新操作写到了一块儿。

# scatter操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//scatter 在[nl,nr]区间内查询sum是否大于等于k
//如果满足条件，设最后一个人在的位置为(row,col)，进行更新
//则[1,row-1]区间内的剩余座位为0，[row,row]区间内剩余座位 减人数
bool do_scatter(int p, int l, int r, int nl, int nr, int k){
    if(T[p].sum<k) return false;//区间内总剩余座位数不够
    
    if(l==r && nr>=r && nl<=l){//该排坐k个人，单点更新
        T[p].sum -= k;
        T[p].maxv = T[p].sum;
        return true;
    }
    int mid=(l+r)>>1;
    //看左子树的总剩余座位数够不够，优先往左子树坐人
    int left = min(T[ls(p)].sum, 1ll*k);//左子树容纳的人数
    
    k -= left;//减去左子树的座位，如果有多的则要去右子树
    bool res = true;
    //左子树不够，还要去右子树，如果加上右子树还不够，返回false
    if(k>0) {
        if(nr<=mid) res=false;//往右子树走需满足 nr>mid
        if(!res) return false;
        res = res && do_scatter(rs(p),mid+1,r,nl,nr,k);
    }
    if(!res) return false;
    //不需要用到右子树，判断左子树是否够
    if(nl<=mid) res = res && do_scatter(ls(p),l,mid,nl,nr,left);
    push_up(p);
    return res;
}

这个操作处理题中的scatter操作，也是将查询和单点更新写在了一块儿。

每次可先判断左子树的总剩余座位数够不够，如果够的话，就不用管右子树了，这些人应该全部往左子树坐；如果不够的话，可以求出右子树要坐的人，再将这些人往右子树坐。

# 代码

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define ll long long 
const int MAXN = 5e4+5;
class BookMyShow {
public:
    int n,m;
    struct node{
        ll sum;//区间内剩余座位的总和
        int maxv;//区间内最大剩余座位数
    }T[MAXN<<2];
    void push_up(int p){
        T[p].sum = T[ls(p)].sum+T[rs(p)].sum;
        T[p].maxv = max(T[ls(p)].maxv, T[rs(p)].maxv);
    }
    void build(int p, int l, int r){
        T[p]={0,0};
        if(l==r){
            T[p]={m,m};//初始时，单排剩余座位为m
            return;
        }
        int mid=(l+r)>>1;
        build(ls(p),l,mid);
        build(rs(p),mid+1,r);
        push_up(p);
    }
    //gather 在[nl,nr]区间内查询第一个剩余座位大于等于k的单点
    //如果找到，还要进行单点更新
    vector<int> do_gather(int p, int l, int r, int nl, int nr, int k){
        if(T[p].maxv < k) return {};//最大容量都满足不了
        
        //l==r说明是单点 nr>=r&&nl<=l说明满足区间要求  找到解了
        if(l==r && nr>=r && nl<=l){
            vector<int> res(2,0);
            res[0] = l-1;
            res[1] = m-T[p].maxv;
            T[p].maxv -= k;//修改
            T[p].sum -= k;
            return res;
        }
        vector<int> ans;
        int mid=(l+r)>>1;
        //要么往左子树走要么往右子树走，直到叶子节点为止
        //如果左子树够的话，肯定先往左子树走；否则往右子树走
        if(T[ls(p)].maxv>=k && nl<=mid) ans = do_gather(ls(p),l,mid,nl,nr,k);
        else if(T[rs(p)].maxv>=k && nr>mid) ans = do_gather(rs(p),mid+1,r,nl,nr,k);
        push_up(p);
        return ans;
    }
    
    //scatter 在[nl,nr]区间内查询sum是否大于等于k
    //如果满足条件，设最后一个人在的位置为(row,col)，进行更新
    //则[1,row-1]区间内的剩余座位为0，[row,row]区间内剩余座位 减人数
    bool do_scatter(int p, int l, int r, int nl, int nr, int k){
        if(T[p].sum<k) return false;//区间内总剩余座位数不够
       
        if(l==r && nr>=r && nl<=l){//该排坐k个人，单点更新
            T[p].sum -= k;
            T[p].maxv = T[p].sum;
            return true;
        }
        int mid=(l+r)>>1;
        //看左子树的总剩余座位数够不够，优先往左子树坐人
        int left = min(T[ls(p)].sum, 1ll*k);//左子树容纳的人数
        
        k -= left;//减去左子树的座位，如果有多的则要去右子树
        bool res = true;
        //左子树不够，还要去右子树，如果加上右子树还不够，返回false
        if(k>0) {
            if(nr<=mid) res=false;//往右子树走需满足 nr>mid
            if(!res) return false;
            res = res && do_scatter(rs(p),mid+1,r,nl,nr,k);
        }
        if(!res) return false;
        //不需要用到右子树，判断左子树是否够
        if(nl<=mid) res = res && do_scatter(ls(p),l,mid,nl,nr,left);
        push_up(p);
        return res;
    }
    BookMyShow(int n, int m) {
        this->n = n;
        this->m = m;
        build(1,1,n);
    }
    
    vector<int> gather(int k, int maxRow) {
        return do_gather(1,1,n,1,maxRow+1,k);
    }
    
    bool scatter(int k, int maxRow) {
        return do_scatter(1,1,n,1,maxRow+1,k);
    }
};

/**
 * Your BookMyShow object will be instantiated and called as such:
 * BookMyShow* obj = new BookMyShow(n, m);
 * vector<int> param_1 = obj->gather(k,maxRow);
 * bool param_2 = obj->scatter(k,maxRow);
 */