
【递归】计算布尔二叉树的值
题目
给你一棵 完整二叉树 的根,这棵树有以下特征:
- 叶子节点 要么值为
0 要么值为 1 ,其中 0 表示 False ,1 表示 True 。 - 非叶子节点 要么值为
2 要么值为 3 ,其中 2 表示逻辑或 OR ,3 表示逻辑与 AND 。
计算 一个节点的值方式如下:
- 如果节点是个叶子节点,那么节点的 值 为它本身,即
True 或者 False 。 - 否则,计算 两个孩子的节点值,然后将该节点的运算符对两个孩子值进行 运算 。
返回根节点 root 的布尔运算值。
完整二叉树 是每个节点有 0 个或者 2 个孩子的二叉树。
叶子节点 是没有孩子的节点。
示例 1:
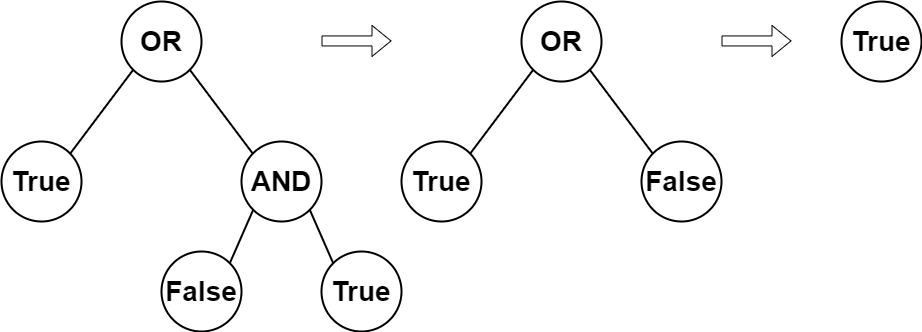
1
2
3
4
5
6
| 输入:root = [2,1,3,null,null,0,1]
输出:true
解释:上图展示了计算过程。
AND 与运算节点的值为 False AND True = False 。
OR 运算节点的值为 True OR False = True 。
根节点的值为 True ,所以我们返回 true 。
|
示例 2:
1
2
3
| 输入:root = [0]
输出:false
解释:根节点是叶子节点,且值为 false,所以我们返回 false 。
|
提示:
- 树中节点数目在
[1, 1000] 之间。 0 <= Node.val <= 3- 每个节点的孩子数为
0 或 2 。 - 叶子节点的值为
0 或 1 。 - 非叶子节点的值为
2 或 3 。
解题思路
按题意递归模拟即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool evaluateTree(TreeNode* root) {
if(root==nullptr) return 0;
bool res;
if(root->left==nullptr && root->right==nullptr){
res = root->val;
return res;
}
if(root->val == 2){
res = evaluateTree(root->left) | evaluateTree(root->right);
}
else if(root->val ==3){
res = evaluateTree(root->left) & evaluateTree(root->right);
}
return res;
}
};
|
【二分 / 贪心+双指针】坐上公交的最晚时间
题目
给你一个下标从 0 开始长度为 n 的整数数组 buses ,其中 buses[i] 表示第 i 辆公交车的出发时间。同时给你一个下标从 0 开始长度为 m 的整数数组 passengers ,其中 passengers[j] 表示第 j 位乘客的到达时间。所有公交车出发的时间互不相同,所有乘客到达的时间也互不相同。
给你一个整数 capacity ,表示每辆公交车 最多 能容纳的乘客数目。
每位乘客都会搭乘下一辆有座位的公交车。如果你在 y 时刻到达,公交在 x 时刻出发,满足 y <= x 且公交没有满,那么你可以搭乘这一辆公交。最早 到达的乘客优先上车。
返回你可以搭乘公交车的最晚到达公交站时间。你 不能 跟别的乘客同时刻到达。
**注意:**数组 buses 和 passengers 不一定是有序的。
示例 1:
1
2
3
4
5
6
| 输入:buses = [10,20], passengers = [2,17,18,19], capacity = 2
输出:16
解释:
第 1 辆公交车载着第 1 位乘客。
第 2 辆公交车载着你和第 2 位乘客。
注意你不能跟其他乘客同一时间到达,所以你必须在第二位乘客之前到达。
|
示例 2:
1
2
3
4
5
6
| 输入:buses = [20,30,10], passengers = [19,13,26,4,25,11,21], capacity = 2
输出:20
解释:
第 1 辆公交车载着第 4 位乘客。
第 2 辆公交车载着第 6 位和第 2 位乘客。
第 3 辆公交车载着第 1 位乘客和你。
|
提示:
n == buses.lengthm == passengers.length1 <= n, m, capacity <= 10^52 <= buses[i], passengers[i] <= 10^9buses 中的元素 互不相同 。passengers 中的元素 互不相同 。
解题思路
赛时有想尝试二分,但是当时觉得check函数不满足二段性,主要是受到了不能跟别的乘客同时刻到达的影响
然后就去做第3题去了
结束后看题解竟然可以二分
check函数判断在k时刻能否搭上公交车,那么在k-1时刻也能搭上公交车;如果在k时刻不能搭上公交车,那么在k+1时刻也不能搭上公交车。(不用考虑和别的乘客同时刻到达的情况,就算同时刻到达,“把他挤下去”,先判断在这个时刻能不能搭上再说)
中间搭车过程用双指针模拟即可,先到车站的先上车
最后如果是已经存在的时刻,则向前减一,直到(且一定)存在一个不存在的时刻
其实也用不到二分,直接用双指针模拟即可,搭上车的两种情况:1)还有空位的情况下,卡点上车;2)挤掉每一辆车的最后上车的那个人
代码
二分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public:
int latestTimeCatchTheBus(vector<int>& buses, vector<int>& passengers, int capacity) {
int n = buses.size();
set<int> tab;
for(auto &x: passengers) tab.insert(x);
sort(buses.begin(),buses.end());
function<bool(int)> check = [&](int k){
vector<int> p(passengers.begin(),passengers.end());
p.push_back(k);
sort(p.begin(),p.end());
int m = p.size();
for(int i=0,j=0;i<n;i++){
int rst = capacity;
while(j<m && p[j]<=buses[i] && rst>0){
if(p[j]==k) return true;//k时间的能搭上公交车
rst--;
j++;
}
}
return false;
};//在k时间是否可以搭上公交
int l=0,r=1e9+5;
while(l<r){
int mid=(l+r)>>1;
if(check(mid)) l=mid+1;
else r=mid;
}
int res = l-1;
while(tab.count(res)) res--;
return res;
}
};
|
贪心+双指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
int latestTimeCatchTheBus(vector<int>& buses, vector<int>& passengers, int capacity) {
int n = buses.size();
int m = passengers.size();
set<int> tab;
for(auto &x: passengers) tab.insert(x);
sort(buses.begin(),buses.end());
sort(passengers.begin(),passengers.end());
int res=-1;
for(int i=0,j=0;i<n;i++){
int rst = capacity;
while(rst>0 && j<m && passengers[j]<=buses[i]){
res = passengers[j];
rst--;
j++;
}
if(rst>0) res = max(res, buses[i]);
}
while(tab.count(res)) res--;
return res;
}
};
|
【贪心/二分】最小差值平方和
题目
给你两个下标从 0 开始的整数数组 nums1 和 nums2 ,长度为 n 。
数组 nums1 和 nums2 的 差值平方和 定义为所有满足 0 <= i < n 的 (nums1[i] - nums2[i])^2 之和。
同时给你两个正整数 k1 和 k2 。你可以将 nums1 中的任意元素 +1 或者 -1 至多 k1 次。类似的,你可以将 nums2 中的任意元素 +1 或者 -1 至多 k2 次。
请你返回修改数组 nums1 至多 k1 次且修改数组 nums2 至多 k2 次后的最小 差值平方和 。
注意: 你可以将数组中的元素变成 负 整数。
示例 1:
1
2
3
4
| 输入:nums1 = [1,2,3,4], nums2 = [2,10,20,19], k1 = 0, k2 = 0
输出:579
解释:nums1 和 nums2 中的元素不能修改,因为 k1 = 0 和 k2 = 0 。
差值平方和为:(1 - 2)^2 + (2 - 10)^2 + (3 - 20)^2 + (4 - 19)^2 = 579 。
|
示例 2:
1
2
3
4
5
6
7
8
| 输入:nums1 = [1,4,10,12], nums2 = [5,8,6,9], k1 = 1, k2 = 1
输出:43
解释:一种得到最小差值平方和的方式为:
- 将 nums1[0] 增加一次。
- 将 nums2[2] 增加一次。
最小差值平方和为:
(2 - 5)^2 + (4 - 8)^2 + (10 - 7)^2 + (12 - 9)^2 = 43 。
注意,也有其他方式可以得到最小差值平方和,但没有得到比 43 更小答案的方案。
|
提示:
n == nums1.length == nums2.length1 <= n <= 10^50 <= nums1[i], nums2[i] <= 10^50 <= k1, k2 <= 10^9
解题思路
先计算a[i] = abs(nums1[i] - nums2[i]),每次操作都是选定一个a[i]进行减一操作
显然,每次减小最大的数的贡献最大,所以原题转化为:
对a[i]>=0,进行k1+k2次操作,每次操作对a[i]-1,求a[i]的最小平方和
所以每次将最高的山峰都消减至次高的山峰即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution {
public:
long long minSumSquareDiff(vector<int>& nums1, vector<int>& nums2, int k1, int k2) {
int n = nums1.size();
int k = k1+k2;
map<int,int,greater<int>> tab;
for(int i=0;i<n;i++){
int cur = abs(nums1[i]-nums2[i]);
tab[cur]++;
}
for(auto it=tab.begin();it!=tab.end();it++){
if(k==0) break;
int u=it->first, cnt = it->second;
auto nit = it;nit++;
int nxt = (nit==tab.end())?0:(nit->first);
// cout<<u<<' '<<nxt<<endl;
int all = (u - nxt)*cnt;
if(k>=all){
k -= all;
tab.erase(u);
tab[nxt] += cnt;
}else{
int layer = k/cnt;
int rst = k%cnt;
if(layer>0){
tab.erase(u);
tab[u-layer] += cnt;
tab[u-layer] -= rst;
tab[u-layer-1] +=rst;
}else{
tab[u] -= rst;
tab[u-1] += rst;
}
break;
}
}
long long ans = 0;
for(auto &x: tab){
ans += 1ll*x.first*x.first*x.second;
//cout<<x.first<<' '<<x.second<<endl;
}
return ans;
}
};
|
二分
先判断是否可以在k步内变成0。
利用二分判断差值数组的每个a[i]的最小目标值u,即a[i] <= u
再看是否有剩余的k
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #define ll long long
class Solution {
public:
long long minSumSquareDiff(vector<int>& nums1, vector<int>& nums2, int k1, int k2) {
int n = nums1.size();
vector<int> a(n);
ll sum=0, k=k1+k2;
for(int i=0;i<n;i++){
a[i] = abs(nums1[i]-nums2[i]);
sum += (a[i]-0);
}
if(sum<=k) return 0;
function<bool(int)> check = [&](int p){
int rst = k;
for(int i=0;i<n;i++){
if(a[i]<=p) continue;
rst -= a[i]-p;
if(rst<0) return false;
}
return true;
};//令每个a[i]<=p 是否ok
int l=0,r=1e5+5;
while(l<r){
int mid=(l+r)>>1;
if(check(mid)) r=mid;
else l=mid+1;
}
int u = r;//最小可以使每个a[i]<=u ,还要看是否有剩余的k
int rst = k;
for(int i=0;i<n;i++){
if(a[i]<=u) continue;
rst -= a[i]-u;
a[i] = u;
}
if(rst){//如果还有剩余的k,一定小于u的数量,每个减一
for(int i=0;i<n;i++){
if(a[i]<u) continue;
a[i]--;
rst--;
if(rst==0) break;
}
}
ll res=0;
for(int i=0;i<n;i++){
res = (res + a[i]*1ll*a[i]);
}
return res;
}
};
|
【单调栈+思维】元素值大于变化阈值的子数组
题目
给你一个整数数组 nums 和一个整数 threshold 。
找到长度为 k 的 nums 子数组,满足数组中 每个 元素都 大于 threshold / k 。
请你返回满足要求的 任意 子数组的 大小 。如果没有这样的子数组,返回 -1 。
子数组 是数组中一段连续非空的元素序列。
示例 1:
1
2
3
4
| 输入:nums = [1,3,4,3,1], threshold = 6
输出:3
解释:子数组 [3,4,3] 大小为 3 ,每个元素都大于 6 / 3 = 2 。
注意这是唯一合法的子数组。
|
示例 2:
1
2
3
4
5
6
| 输入:nums = [6,5,6,5,8], threshold = 7
输出:1
解释:子数组 [8] 大小为 1 ,且 8 > 7 / 1 = 7 。所以返回 1 。
注意子数组 [6,5] 大小为 2 ,每个元素都大于 7 / 2 = 3.5 。
类似的,子数组 [6,5,6] ,[6,5,6,5] ,[6,5,6,5,8] 都是符合条件的子数组。
所以返回 2, 3, 4 和 5 都可以。
|
提示:
1 <= nums.length <= 10^51 <= nums[i], threshold <= 10^9
解题思路
要使得数组中每个元素都大于threshold/k,即数组中的最小值大于threshold/k
对于k’ > k, 有threshold/k’ < threshold/k
因此考虑以nums[i]为最小值的子数组,找出其最长子数组的长度m,如果有nums[i] > threshold/m,则m满足题意
利用单调栈找出以nums[i]为最小值的子数组的范围
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public:
int validSubarraySize(vector<int>& nums, int threshold) {
int n = nums.size();
vector<int> L(n,-1),R(n,n);//两侧第一个比nums[i]小的元素
stack<int> stk;
for(int i=0;i<n;i++){
while(!stk.empty() && nums[stk.top()]>=nums[i]) stk.pop();
if(stk.empty()) L[i]=-1;
else L[i]=stk.top();
stk.push(i);
}
while(!stk.empty()) stk.pop();
for(int i=n-1;i>=0;i--){
while(!stk.empty() && nums[stk.top()]>=nums[i]) stk.pop();
if(stk.empty()) R[i]=n;
else R[i]=stk.top();
stk.push(i);
}
for(int i=0;i<n;i++){
int m = R[i]-1 - (L[i]+1) + 1;//以nums[i]为最小值的区间的长度
if(1ll*nums[i] * m > 1ll*threshold) return m;
}
return -1;
}
};
|


