没打
【找规律】分割圆的最少切割次数
题目
圆内一个 有效切割 ,符合以下二者之一:
- 该切割是两个端点在圆上的线段,且该线段经过圆心。
- 该切割是一端在圆心另一端在圆上的线段。
一些有效和无效的切割如下图所示。
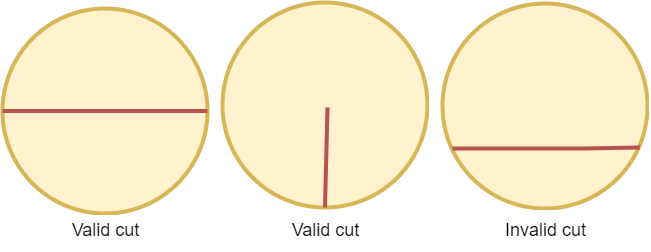
给你一个整数 n ,请你返回将圆切割成相等的 n 等分的 最少 切割次数。
示例 1:
1
2
3
4
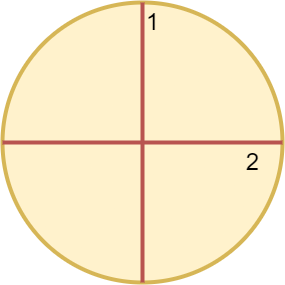
| 输入:n = 4
输出:2
解释:
上图展示了切割圆 2 次,得到四等分。
|
示例 2:
1
2
3
4
5
6
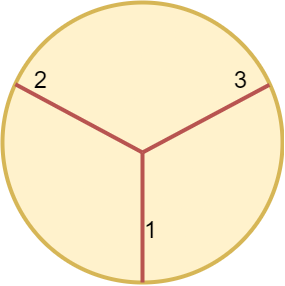
| 输入:n = 3
输出:3
解释:
最少需要切割 3 次,将圆切成三等分。
少于 3 次切割无法将圆切成大小相等面积相同的 3 等分。
同时可以观察到,第一次切割无法将圆切割开。
|
提示:
解题思路
枚举前几个可以发现规律
代码
1
2
3
4
5
6
7
8
| class Solution {
public:
int numberOfCuts(int n) {
if(n==1) return 0;
if(n%2==0) return n/2;
return n;
}
};
|
【模拟】行和列中一和零的差值
题目
给你一个下标从 0 开始的 m x n 二进制矩阵 grid 。
我们按照如下过程,定义一个下标从 0 开始的 m x n 差值矩阵 diff :
- 令第
i 行一的数目为 onesRowi 。 - 令第
j 列一的数目为 onesColj 。 - 令第
i 行零的数目为 zerosRowi 。 - 令第
j 列零的数目为 zerosColj 。 diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj
请你返回差值矩阵 diff 。
示例 1:
1
2
3
4
5
6
7
8
9
10
11
12
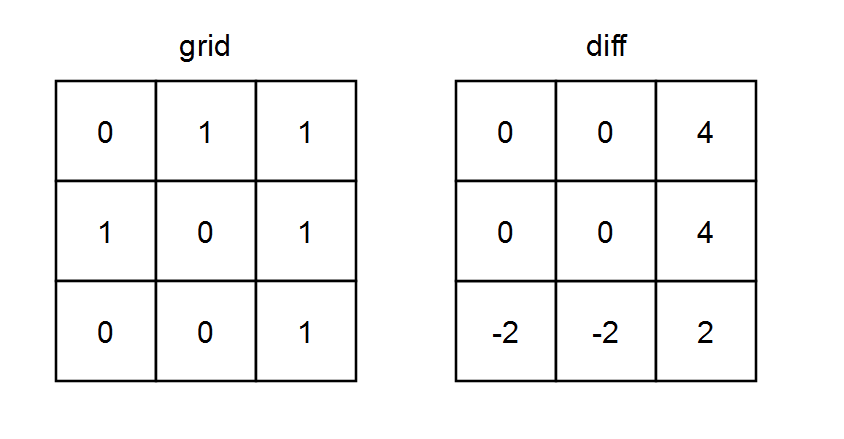
| 输入:grid = [[0,1,1],[1,0,1],[0,0,1]]
输出:[[0,0,4],[0,0,4],[-2,-2,2]]
解释:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 2 + 1 - 1 - 2 = 0
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 2 + 1 - 1 - 2 = 0
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 2 + 3 - 1 - 0 = 4
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 2 + 1 - 1 - 2 = 0
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 2 + 1 - 1 - 2 = 0
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 2 + 3 - 1 - 0 = 4
- diff[2][0] = onesRow2 + onesCol0 - zerosRow2 - zerosCol0 = 1 + 1 - 2 - 2 = -2
- diff[2][1] = onesRow2 + onesCol1 - zerosRow2 - zerosCol1 = 1 + 1 - 2 - 2 = -2
- diff[2][2] = onesRow2 + onesCol2 - zerosRow2 - zerosCol2 = 1 + 3 - 2 - 0 = 2
|
示例 2:
1
2
3
4
5
6
7
8
9
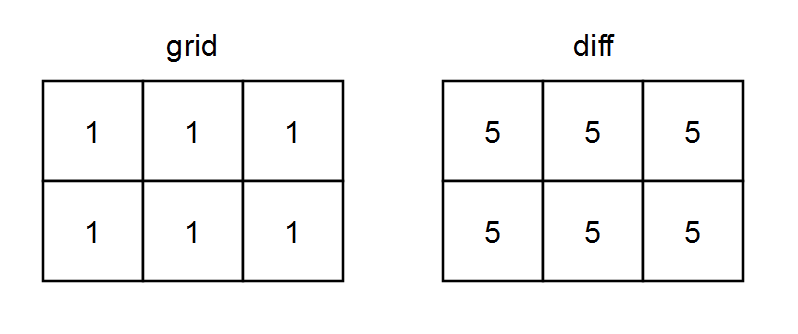
| 输入:grid = [[1,1,1],[1,1,1]]
输出:[[5,5,5],[5,5,5]]
解释:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5
|
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10^51 <= m * n <= 10^5grid[i][j] 要么是 0 ,要么是 1 。
解题思路
按题意模拟即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
vector<vector<int>> onesMinusZeros(vector<vector<int>>& g) {
int n = g.size(), m = g[0].size();
vector<int> onesRow(n,0),onesCol(m,0),zeroRow(n,0),zeroCol(m,0);
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
onesRow[i] += g[i][j];
}
zeroRow[i] = m - onesRow[i];
}
for(int j=0;j<m;j++){
for(int i=0;i<n;i++){
onesCol[j] += g[i][j];
}
zeroCol[j] = n - onesCol[j];
}
vector<vector<int>> res(n, vector<int>(m,0));
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
res[i][j] = onesRow[i]+onesCol[j]-zeroRow[i]-zeroCol[j];
}
}
return res;
}
};
|
【枚举+前缀和】商店的最少代价
题目
给你一个顾客访问商店的日志,用一个下标从 0 开始且只包含字符 'N' 和 'Y' 的字符串 customers 表示:
- 如果第
i 个字符是 'Y' ,它表示第 i 小时有顾客到达。 - 如果第
i 个字符是 'N' ,它表示第 i 小时没有顾客到达。
如果商店在第 j 小时关门(0 <= j <= n),代价按如下方式计算:
- 在开门期间,如果某一个小时没有顾客到达,代价增加
1 。 - 在关门期间,如果某一个小时有顾客到达,代价增加
1 。
请你返回在确保代价 最小 的前提下,商店的 最早 关门时间。
注意,商店在第 j 小时关门表示在第 j 小时以及之后商店处于关门状态。
示例 1:
1
2
3
4
5
6
7
8
9
| 输入:customers = "YYNY"
输出:2
解释:
- 第 0 小时关门,总共 1+1+0+1 = 3 代价。
- 第 1 小时关门,总共 0+1+0+1 = 2 代价。
- 第 2 小时关门,总共 0+0+0+1 = 1 代价。
- 第 3 小时关门,总共 0+0+1+1 = 2 代价。
- 第 4 小时关门,总共 0+0+1+0 = 1 代价。
在第 2 或第 4 小时关门代价都最小。由于第 2 小时更早,所以最优关门时间是 2 。
|
示例 2:
1
2
3
| 输入:customers = "NNNNN"
输出:0
解释:最优关门时间是 0 ,因为自始至终没有顾客到达。
|
示例 3:
1
2
3
| 输入:customers = "YYYY"
输出:4
解释:最优关门时间是 4 ,因为每一小时均有顾客到达。
|
提示:
1 <= customers.length <= 10^5customers 只包含字符 'Y' 和 'N' 。
解题思路
枚举即可,前缀和优化
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public:
int bestClosingTime(string customers) {
int n = customers.size();
vector<int> yes(n+1,0),no(n+1,0);
for(int i=1;i<=n;i++){
if(customers[i-1]=='Y') yes[i] = yes[i-1]+1, no[i] = no[i-1];
else yes[i] = yes[i-1], no[i] = no[i-1] + 1;
}
int minv = yes[n], idx = 0;
for(int i=1;i<=n;i++){
int u = no[i] + yes[n] - yes[i];
if(u<minv){
minv = u;
idx = i;
}
}
return idx;
}
};
|
【DP+计数】统计回文子序列数目
题目
给你数字字符串 s ,请你返回 s 中长度为 5 的 回文子序列 数目。由于答案可能很大,请你将答案对 109 + 7 取余 后返回。
提示:
- 如果一个字符串从前往后和从后往前读相同,那么它是 回文字符串 。
- 子序列是一个字符串中删除若干个字符后,不改变字符顺序,剩余字符构成的字符串。
示例 1:
1
2
3
4
5
| 输入:s = "103301"
输出:2
解释:
总共有 6 长度为 5 的子序列:"10330" ,"10331" ,"10301" ,"10301" ,"13301" ,"03301" 。
它们中有两个(都是 "10301")是回文的。
|
示例 2:
1
2
3
| 输入:s = "0000000"
输出:21
解释:所有 21 个长度为 5 的子序列都是 "00000" ,都是回文的。
|
示例 3:
1
2
3
| 输入:s = "9999900000"
输出:2
解释:仅有的两个回文子序列是 "99999" 和 "00000" 。
|
提示:
1 <= s.length <= 10^4s 只包含数字字符。
解题思路
对应低配题:https://leetcode.cn/problems/unique-length-3-palindromic-subsequences/
枚举中心点,统计前面和后面两种字符的组合即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| const int MOD = 1e9+7;
class Solution {
public:
int countPalindromes(string s) {
int n = s.size();
int suf_one[10];// suf_one[i] 表示 当前s[..n]中i的个数
int suf_two[10][10];// suf_two[i][j] 表示 当前s[..n]中i j的个数
memset(suf_one,0,sizeof(suf_one));
memset(suf_two,0,sizeof(suf_two));
suf_one[s[n-1]-'0'] = 1;
for(int i=n-2;i>0;i--){
for(int j=0;j<10;j++){
suf_two[s[i]-'0'][j] += suf_one[j];
}
suf_one[s[i]-'0'] ++;
}
int pre_one[10];
int pre_two[10][10];
memset(pre_one,0,sizeof(pre_one));
memset(pre_two,0,sizeof(pre_two));
int res = 0;
pre_one[s[0]-'0'] = 1;
for(int i=1;i<n;i++){
suf_one[s[i]-'0'] -= 1;
for(int j=0;j<10;j++){
suf_two[s[i]-'0'][j] -= suf_one[j];
}
for(int j=0;j<10;j++){
for(int k=0;k<10;k++){
if(pre_two[j][k] && suf_two[k][j]){//j k s[i] k j
res = (res + 1ll*pre_two[j][k]*suf_two[k][j]) % MOD;
}
}
}
for(int j=0;j<10;j++){
pre_two[j][s[i]-'0'] += pre_one[j];
}
pre_one[s[i]-'0'] += 1;
}
return res;
}
};
|





