没打
【枚举】有效时间的数目
题目
给你一个长度为 5 的字符串 time ,表示一个电子时钟当前的时间,格式为 "hh:mm" 。最早 可能的时间是 "00:00" ,最晚 可能的时间是 "23:59" 。
在字符串 time 中,被字符 ? 替换掉的数位是 未知的 ,被替换的数字可能是 0 到 9 中的任何一个。
请你返回一个整数 answer ,将每一个 ? 都用 0 到 9 中一个数字替换后,可以得到的有效时间的数目。
示例 1:
1
2
3
| 输入:time = "?5:00"
输出:2
解释:我们可以将 ? 替换成 0 或 1 ,得到 "05:00" 或者 "15:00" 。注意我们不能替换成 2 ,因为时间 "25:00" 是无效时间。所以我们有两个选择。
|
示例 2:
1
2
3
| 输入:time = "0?:0?"
输出:100
解释:两个 ? 都可以被 0 到 9 之间的任意数字替换,所以我们总共有 100 种选择。
|
示例 3:
1
2
3
| 输入:time = "??:??"
输出:1440
解释:小时总共有 24 种选择,分钟总共有 60 种选择。所以总共有 24 * 60 = 1440 种选择。
|
提示:
time 是一个长度为 5 的有效字符串,格式为 "hh:mm" 。"00" <= hh <= "23""00" <= mm <= "59"- 字符串中有的数位是
'?' ,需要用 0 到 9 之间的数字替换。
解题思路
枚举即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
public:
int trans(string time){
int res = 0;
res += time[4]-'0';
if(time[3]>'5') return -1;
res += (time[3]-'0')*10;
int hour = 10*(time[0]-'0')+(time[1]-'0');
if(time[0]>'2') return -1;
if(time[0]=='2' && time[1]>'3') return -1;
res += hour*60;
return res;
}
int countTime(string time) {
vector<int> a(5,0);
for(int i=0;i<5;i++){
if(time[i]=='?') a[i] = 1;
}
int res = 0;
function<void(int,string)> dfs = [&](int pos,string ctime)->void{
if(pos==5){
// cout<<ctime<<' '<<trans(ctime)<<endl;
if(trans(ctime)>-1 && trans(ctime)<=1440) res++;
return;
}
if(a[pos]){
for(int d=0;d<10;d++){
ctime[pos] = char(d+'0');
dfs(pos+1, ctime);
}
}else dfs(pos+1,ctime);
return;
};
dfs(0,time);
return res;
}
};
|
【快速幂】二的幂数组中查询范围内的乘积
题目
给你一个正整数 n ,你需要找到一个下标从 0 开始的数组 powers ,它包含 最少 数目的 2 的幂,且它们的和为 n 。powers 数组是 非递减 顺序的。根据前面描述,构造 powers 数组的方法是唯一的。
同时给你一个下标从 0 开始的二维整数数组 queries ,其中 queries[i] = [lefti, righti] ,其中 queries[i] 表示请你求出满足 lefti <= j <= righti 的所有 powers[j] 的乘积。
请你返回一个数组 answers ,长度与 queries 的长度相同,其中 answers[i]是第 i 个查询的答案。由于查询的结果可能非常大,请你将每个 answers[i] 都对 109 + 7 取余 。
示例 1:
1
2
3
4
5
6
7
8
| 输入:n = 15, queries = [[0,1],[2,2],[0,3]]
输出:[2,4,64]
解释:
对于 n = 15 ,得到 powers = [1,2,4,8] 。没法得到元素数目更少的数组。
第 1 个查询的答案:powers[0] * powers[1] = 1 * 2 = 2 。
第 2 个查询的答案:powers[2] = 4 。
第 3 个查询的答案:powers[0] * powers[1] * powers[2] * powers[3] = 1 * 2 * 4 * 8 = 64 。
每个答案对 109 + 7 得到的结果都相同,所以返回 [2,4,64] 。
|
示例 2:
1
2
3
4
5
| 输入:n = 2, queries = [[0,0]]
输出:[2]
解释:
对于 n = 2, powers = [2] 。
唯一一个查询的答案是 powers[0] = 2 。答案对 109 + 7 取余后结果相同,所以返回 [2] 。
|
提示:
1 <= n <= 10^91 <= queries.length <= 10^50 <= starti <= endi < powers.length
解题思路
预处理出2的幂的指数的前缀和 再利用快速幂即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #define ll long long
class Solution {
public:
ll quickpower(ll x,ll y,int mod){//x^y % mod
ll res = 1;
while(y>0){
if(y&1) res = (res*x)%mod;
x = (x*x)%mod;
y>>=1;
}
return res;
}
vector<int> productQueries(int n, vector<vector<int>>& queries) {
vector<int> powers;
for(int i=0;i<32;i++){
if((n>>i)&1) powers.push_back(i);
}
// for(auto &x: powers) cout<<x<<' ';
int m = powers.size();
vector<int> sum(m+1,0),res;
for(int i=1;i<=m;i++) sum[i] = sum[i-1]+powers[i-1];
for(auto &vec: queries){
int cnt = sum[vec[1]+1]-sum[vec[0]];
res.push_back(quickpower(2,cnt,1e9+7));
}
return res;
}
};
|
【二分】最小化数组中的最大值
题目
给你一个下标从 0 开始的数组 nums ,它含有 n 个非负整数。
每一步操作中,你需要:
- 选择一个满足
1 <= i < n 的整数 i ,且 nums[i] > 0 。 - 将
nums[i] 减 1 。 - 将
nums[i - 1] 加 1 。
你可以对数组执行 任意 次上述操作,请你返回可以得到的 nums 数组中 最大值 最小 为多少。
示例 1:
1
2
3
4
5
6
7
8
9
| 输入:nums = [3,7,1,6]
输出:5
解释:
一串最优操作是:
1. 选择 i = 1 ,nums 变为 [4,6,1,6] 。
2. 选择 i = 3 ,nums 变为 [4,6,2,5] 。
3. 选择 i = 1 ,nums 变为 [5,5,2,5] 。
nums 中最大值为 5 。无法得到比 5 更小的最大值。
所以我们返回 5 。
|
示例 2:
1
2
3
4
| 输入:nums = [10,1]
输出:10
解释:
最优解是不改动 nums ,10 是最大值,所以返回 10 。
|
提示:
n == nums.length2 <= n <= 10^50 <= nums[i] <= 10^9
解题思路
最小化最大值 想到二分,即二分这个最大值res
res的可从[0, maxv]二分搜索
在O(n)时间内判断最大值为res时是否合法
每次操作是将后一个元素减1,加到前一个元素上
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
class Solution {
public:
int minimizeArrayValue(vector<int>& nums) {
int n = nums.size();
function<bool(int)> isok = [&](int k)->bool{
ll rst = 0;
for(int i=n-1;i>=1;i--){
if(rst + nums[i] > k) rst = rst + nums[i] - k;
else rst = 0;
}
if(nums[0]+rst>k) return false;
else return true;
};
int l = 0, r = *max_element(nums.begin(),nums.end());
while(l<r){
int mid=(l+r)>>1;
if(isok(mid)) r = mid;
else l=mid+1;
}
return r;
}
};
|
【枚举+dfs树上统计】创建价值相同的连通块
题目
有一棵 n 个节点的无向树,节点编号为 0 到 n - 1 。
给你一个长度为 n 下标从 0 开始的整数数组 nums ,其中 nums[i] 表示第 i 个节点的值。同时给你一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 与 bi 之间有一条边。
你可以 删除 一些边,将这棵树分成几个连通块。一个连通块的 价值 定义为这个连通块中 所有 节点 i 对应的 nums[i] 之和。
你需要删除一些边,删除后得到的各个连通块的价值都相等。请返回你可以删除的边数 最多 为多少。
示例 1:
1
2
3
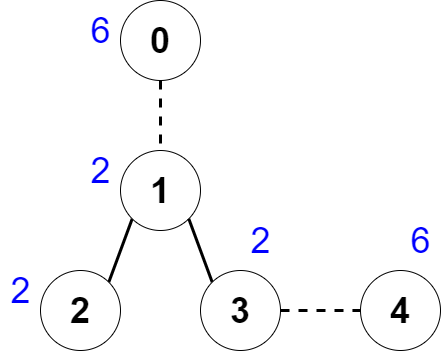
| 输入:nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]]
输出:2
解释:上图展示了我们可以删除边 [0,1] 和 [3,4] 。得到的连通块为 [0] ,[1,2,3] 和 [4] 。每个连通块的价值都为 6 。可以证明没有别的更好的删除方案存在了,所以答案为 2 。
|
示例 2:
1
2
3
| 输入:nums = [2], edges = []
输出:0
解释:没有任何边可以删除。
|
提示:
1 <= n <= 2 * 10^4nums.length == n1 <= nums[i] <= 50edges.length == n - 1edges[i].length == 20 <= edges[i][0], edges[i][1] <= n - 1edges 表示一棵合法的树。
解题思路
主要思路是枚举可以划分的联通块块数
所有权值的和sum最大为10^6,可以划分的联通块的权值即是sum的因子,数字x的因子个数可近似估计为x开立方。实际上10^6的因子个数为240。
那么枚举sum的因子target,然后再在O(n)时间内判断是否可以划分出权值总和为target的连通块即可
利用dfs在树上统计,详见代码
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public:
int componentValue(vector<int>& nums, vector<vector<int>>& edges) {
int n = nums.size();
vector<int> G[n];
for(auto &vec: edges){
G[vec[0]].push_back(vec[1]);
G[vec[1]].push_back(vec[0]);
}
int sum = accumulate(nums.begin(),nums.end(),0);
function<int(int,int,int)> dfs = [&](int u, int fa, int target)->int{
int s = nums[u];
for(auto &v: G[u]){
if(v == fa) continue;
int ss = dfs(v,u,target);
if(ss==-1) return -1;
s += ss;
}
if(s == target) return 0;//连通块总和为target,赋值为0表示删去
else if(s>target) return -1;//连通块总和大于target,肯定有一个连通块权值和大于target了,非法
return s;
};//以u为根节点的子树,是否可以分成价值总和为target的连通块,等于则0
for(int i=n;i>=1;i--){//枚举分成i个联通块
if(sum%i==0){
if(dfs(0,-1, sum/i) == 0){
return i-1;
}
}
}
return 0;
}
};
|

